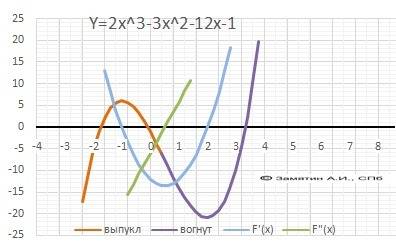
ДАНО:Y = 2*x³ - 3*x² - 12*x - 1 - функция
ИССЛЕДОВАТЬ.
1. Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
2. Пересечение с осью Х. Y=0 при х₁ = - 1,76, Х₂ = - 0,09, Х₃ = 3,34
Положительна - X∈(Х₁;Х₂)∪(Х₃;+∞), отрицательна - X∈(-∞;Х₁)∪(Х₂;Х₃).
3. Пересечение с осью У. У(0) = -1.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞
5. Исследование на чётность.Y(-x) ≠ Y(x). Y(-x) ≠ -Y(x),
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 6*x² -6*Х - 12 = 6*(x-2)(x+1).
Корни при Х₁= 2, Х₂ = -1 Схема знаков производной.
(-∞)__(>0)__(-1)___(<0)___(2)__(>0)_____(+∞)
7. Локальные экстремумы.
Максимум Ymax(-1)= 6 , минимум – Ymin(2) = - 21.
8. Интервалы возрастания и убывания.
Возрастает - Х∈[-∞; -1]∪[2;+∞), убывает = Х∈(-1; 2).
8. Вторая производная - Y"(x) = 12*x - 6=0.
Корень производной - точка перегиба Y"(x)= 0.5.
9. Выпуклая “горка» Х∈(-∞; 0.5), Вогнутая – «ложка» Х∈(0.5; +∞).
10. График в приложении.
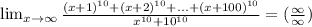
1) Используя бином Ньютона, возведем в 10-ую степень первое слагаемое числителя:
(x+1)¹⁰=х¹⁰+10х⁹+45x⁸+120x⁷+210x⁶+25x⁵+210x⁴+120x³+45x²+10x+1
У данного разложения старшая степень х¹⁰ имеет коэффициент, равный 1.
Аналогично можно возводить в 10-ую степень и остальные слагаемые. НО делать этого не нужно, т.к. очевидно, что у каждого слагаемого при разложении старшая степень х¹⁰ имеет коэффициент равный 1.
2) Всего в числителе 100 слагаемых, таким образом получаем сумму старших степеней с коэффициентом, равным 100.
х¹⁰+х¹⁰+...+х¹⁰ = 100х¹⁰
3) Теперь возвратимся к данному пределу, оставив только старшие степени числителя и знаменателя:
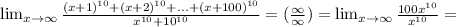
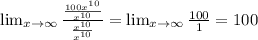
надо каждое число,которое стоит в скобках умножить на число,которое стоит за скобкой