 . Решение:
. Решение: Составим "порядок действий" к задаче:
Вначале посчитаем (перечислим), сколько всего исходов может быть, если на всех трех кубиках выпали разные грани. Это будет несложно сделать, если мы будем считать, что порядок значения не имеет (если же мы будем считать, что порядок имеет значение, то получим тоже самое).А потом посчитаем, в скольких из этих присутствует единица.Найдем отношение второго к первому, то есть вероятность.Итак, перечислим исходы, если на всех кубиках выпало разное число очков, без учета порядка:
123, 124, 125, 126, 134, 135, 136, 145, 146, 156,
234, 235, 236, 245, 246, 256, 345, 346, 356, 456.
В первой строке - все исходы, в которых выпадает 1; их всего 10. Во второй строке оставшиеся исходы, их тоже 10.
Значит:
Р (выпала единица | на всех трёх костях выпали разные грани) =
= 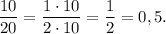
Задача решена!
P.S. Задачу можно решить целиком через условную вероятность, как я сделала вначале, но это значительно скучнее, чем так. И результаты, кажется, совпадают.
 Решение:
Решение:Известно, что орел выпал по меньшей мере три раза подряд. Это означает, что он выпал 3, 4 или 5 раз подряд.
Если орел (герб) выпал 3 раза подряд, нам подходят следующие комбинации (О=орел, Р=решка):
ОООРР, ОООРО, РОООР, РРООО, ОРООО. (5)
Если 4 раза подряд:
ООООР, РОООО. (2)
А если уж 5 раз подряд, то комбинация только одна:
ООООО. (1)
Всего подходящих (благоприятствующих) комбинаций:
1 + 2 + 5 = 8.
А вообще всех комбинаций можно насчитать (если постараться):
2 · 2 · 2 · 2 · 2 = 32.
И тогда вероятность равна:
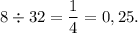
Задача решена!
а) Дроби:1/2, 3/4, 5/8, 7/12. приведите к знаменателю 24
б) Дроби: 1/2, 1/3, 2/9, 5/18. приведите к знаменателю 36