1) Дать определение: число a больше числа b
a > b, ели a − b > 0
Число a больше числа b, если разность этих чисел положительна.
2) Сравнить:
а)
8/11 и 9/13
Вычтем из первого числа второе:
 и 0
и 0
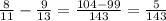
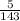 и 0
и 0
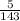 > 0
> 0
Значит, 
б)
a²+16 и 8a
Вычтем из первого выражения второе:
a²−8a+16 и 0
(a−4)² и 0
по определению, вырежение в квадрате всегда дает число неотрицательное, то есть (a−4)²≥0
(a−4)² = 0, если a = 4
(a−4)² > 0, если a ≠ 4
Значит, a² + 16 > 8a, если a ≠ 4; и a²+16 = 8a, если a = 4.
3) Доказать неравенство:
(a−3)(a+11) < (a+3)(a+5)
a²+11a−3a−33 < a²+5a+3a+15
Вычтем из первого выражения второе:
a²+11a−3a−33−a²−5a−3a−15 и 0
−48 и 0
Значит, (a−3)(a+11) < (a+3)(a+5), что и требовалось доказать.
4) Сравнить числа а и b, если верно неравенство: 3a−3b ≥ 1
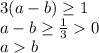
5) Оценить величину: 5а−2, если 1,1 < а ≤ 1,2
Умножим все части неравенства на 5:
5·1,1 < 5a ≤ 5·1,2
5,5 < 5а ≤ 6
Вычтем из всех частей неравенства 2:
5,5−2 < 5а−2 ≤ 6−2
Получаем:
3,5 < 5а−2 ≤ 4
ответ:
пошаговое объяснение:
1) область определения функции. точки разрыва функции.
2) четность или нечетность функции.
y(-x)=x3-3·x-2
функция общего вида
3) периодичность функции.
4) точки пересечения кривой с осями координат.
пересечение с осью 0y
x=0, y=-2
пересечение с осью 0x
y=0
-x3+3·x-2=0
x1=-2, x2=1
5) исследование на экстремум.
y = -x^3+3*x-2
1. находим интервалы возрастания и убывания. первая производная.
f'(x) = -3·x2+3
находим нули функции. для этого приравниваем производную к нулю
-3·x2+3 = 0
откуда:
x1 = -1
x2 = 1
(-∞ ; -1) (-1; 1) (1; +∞)
f'(x) < 0 f'(x) > 0 f'(x) < 0
функция убывает функция возрастает функция убывает
в окрестности точки x = -1 производная функции меняет знак с (-) на (+). следовательно, точка x = -1 - точка минимума. в окрестности точки x = 1 производная функции меняет знак с (+) на (-). следовательно, точка x = 1 - точка максимума.
2. найдем интервалы выпуклости и вогнутости функции. вторая производная.
f''(x) = -6·x
находим корни уравнения. для этого полученную функцию приравняем к нулю.
-6·x = 0
откуда точки перегиба:
x1 = 0
(-∞ ; 0) (0; +∞)
f''(x) > 0 f''(x) < 0
функция вогнута функция выпукла
6) асимптоты кривой.
y = -x3+3·x-2
уравнения наклонных асимптот обычно ищут в виде y = kx + b. по определению асимптоты:
находим коэффициент k:
поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.
ответ: Лена за лето прочитала 6 книг.