Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -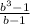
· X
После четвертой выплаты сумма оставшегося долга равна:
S4 =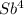 
- (1 + b +b² + b³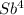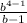)X = 
- 
· X
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому 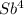- 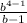· X = 0.
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X = 
рублей
1. у=-3х+1. Это монотонно убывающая функция, поэтому наибольшее и наименьшее значения достигаются на концах отрезка.
Наибольшее значения: у (-2) = (-3)*(-2) + 1 =7
Наименьшее значение: у (1) = (-3)*(1) + 1 = -2.
2. Находим вершину параболы: у=х²-4х +4 -4 = (х-2)² - 4, т. е вершина находится в точке х=2, при этом функция достигает наименьшего значения у= -4. Оно же будет наименьшим на отрезке [0:3]. Наибольшее будет при х=0 (т. к. эта точка дальше отстоит от вершины, чем х=3). при этом у (0) = 8
Пошаговое объяснение:
