Найдем вероятность того, что при восьми бросках ни разу не выпадет простое число очков.
При единичном броске эта вероятность равна (так как всего результатом могут стать шесть цифр: 1, 2, 3, 4, 5, 6; а простых из них всего лишь три: 2, 3, 5).
А так как бросков было совершено восемь, то:
P (ни разу не выпадет простое число очков) = .
Заметим, что мы искали вероятность события, противоположного искомому. Поэтому вероятность искомого события равна:
ответ: 255 / 256 или 0,99609375 . №2.
Найдем вероятность того, что ни разу не выпадет ни 1 очко, ни 6 очков.
При единичном броске мы имеем четыре благоприятствующих исхода (2, 3, 4, 5) из шести возможных (1, 2, 3, 4, 5, 6). Вероятность равна .
При восьми бросках, естественно, получается .
И вероятность искомого события (противоположного рассматриваемому) равна:
Что такое дробь? Когда возникла необходимость делить целое на части без лишних усилий, тогда и появились дроби. История дробей неразрывна связана с решением утилитарных задач. Сам термин «дробь» имеет арабские корни и происходит от слова, обозначающего «ломать, разделять». С древних времен в этом смысле мало что изменилось. Современное определение звучит следующим образом: дробь — это часть или сумма частей единицы. Соответственно, примеры с дробями представляют собой последовательное выполнение математических операций с долями чисел.Пришли из глубины веков Впервые оперировать дробями начали на территории Египта и Вавилона. Подход математиков двух государств имел значительные отличия. Однако начало и там и там было положено одинаково. Первой дробью стала половина или 1/2. Дальше возникла четверть, треть и так далее. Согласно данным археологических раскопок, история возникновения дробей насчитывает около 5 тысяч лет. Впервые доли числа встречаются в египетских папирусах и на вавилонских глиняных табличках.
Необходимость в дробных числах возникла у человека на весьма ранней стадии развития. Уже дележ добычи, состоявший из нескольких убитых животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе.
Наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удаётся выразить натуральным числом, приходится учитывать и части употребляемой меры. Исторически дроби возникли в процессе измерения.
Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей.
В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, два с половиной шага. Откуда можно было сделать вывод, что дробные числа возникли как результат измерения величин. Народы через многие варианты записи дробей, пока не пришли к современной записи.
Найдем вероятность того, что при восьми бросках ни разу не выпадет простое число очков.
При единичном броске эта вероятность равна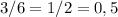 (так как всего результатом могут стать шесть цифр: 1, 2, 3, 4, 5, 6; а простых из них всего лишь три: 2, 3, 5).
(так как всего результатом могут стать шесть цифр: 1, 2, 3, 4, 5, 6; а простых из них всего лишь три: 2, 3, 5).
А так как бросков было совершено восемь, то:
P (ни разу не выпадет простое число очков) =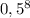 .
.
Заметим, что мы искали вероятность события, противоположного искомому. Поэтому вероятность искомого события равна:
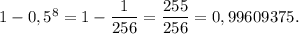
ответ: 255 / 256 или 0,99609375 . №2.Найдем вероятность того, что ни разу не выпадет ни 1 очко, ни 6 очков.
При единичном броске мы имеем четыре благоприятствующих исхода (2, 3, 4, 5) из шести возможных (1, 2, 3, 4, 5, 6). Вероятность равна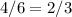 .
.
При восьми бросках, естественно, получается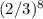 .
.
И вероятность искомого события (противоположного рассматриваемому) равна:
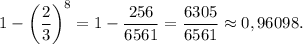
ответ: 6305 / 6561 или около 0,96098.