Пошаговое объяснение:
Пусть Джо поставит вначале 1 доллар. Если выиграет, пусть он скажет "хорошо" и снова поставит 1 доллар. Если проиграет, то в следующей ставке он ставит 2 доллара. Если он выигрывает, то его выигрыш покроет предыдущий проигрыш, и по сумме двух ставок он выиграет 1 доллар. После этого пусть Джо снова скажет "хорошо" и в новой ставке ставит 1 доллар. Если он проиграет и во второй раз, в третий раз он поставит 4 доллара, чтобы в случае выигрыша покрыть предыдущие проигрыши. Если проигрывает в третий раз, то в четвертый раз ставит 8 долларов, если проигрывает и в четвертый, то в пятый раз ставит 16 долларов. По условию он не проигрывает пять раз подряд, значит играя таким образом до первого выигрыша, он заработает 1 доллар не более, чем за 5 ставок. После этого он скажет "хорошо" и будет ставить также, как вначале.
Итак, после 1000 "хорошо" Джо выиграет 1000 долларов. Для этого ему потребуется сделать не более 5000 ставок.
10. У нас дано, что A⊂B.
Докажем, что (C\B)⊂(C\A).
Доказательство.
Пусть x∈C\B, тогда x∈C и x∉B,
если x∉B, то (т.к. A⊂B) x∉A, имеем
x∈C и x∉A, => x∈C\A.
чтд.
11. Доказательство "⇒".
Пусть у нас дано (A∪B = A∩B), докажем тогда, что A = B.
Доказательсво. Пусть x∈A, тогда x∈AUB, но т.к. A∪B = A∩B, то
x∈A∩B, и т.к. A∩B⊂B, имеем x∈B. Мы доказали сейчас, что А⊂B.
Теперь докажем, что B⊂A. Доказательство аналогичное:
пусть x∈B, => x∈A∪B, т.к. A∪B = A∩B, то x∈A∩B, т.к. A∩B⊂A, => x∈A.
Итак, B⊂A.
Т.к. A⊂B и B⊂A, ⇔ A = B. чтд.
Доказательство "<=".
Пусть у нас дано A = B, докажем тогда, что A∪B = A∩B.
Если A = B, то A∪B = B∪B = B, и A∩B = B∩B = B,
то есть A∪B = B = A∩B.
чтд.
12. Доказательство "=>"
Пусть у нас дано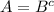 
, докажем тогда, что
(A∩B = ∅) и (A∪B = U).
Доказательство. 
это по определению есть U\B, где U - универсальное множество, то есть у нас дано
A = U\B, тогда
A∩B = (U\B)∩B,
если x∈A∩B, то x∈A и x∈B, то есть x∈U\B и x∈B, то есть
x∈U и x∉B, и x∈B,
x не может одновременно и принадлежать B и не принадлежать B, то есть такого x не существует, то есть x∈∅, мы доказали, что A∩B ⊂∅, но тогда A∩B = ∅.
теперь докажем, что A∪B = U,
Очевидно, что A∪B ⊂U,
докажем, что U⊂A∪B (при условии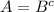 
).
если x∈U, тогда x∈B или x∉B,
( если x∉B, тогда x∈ ), имеем
x∈B или x∈
но т.к.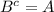 
имеем
x∈B или x∈A, то есть
x∈A∪B.
Мы доказали, что U⊂A∪B, и что A∪B⊂U (очевидное утверждение)
Итак, A∪B = U.
Доказательство "<=".
Пусть у нас дано: (A∩B = ∅) и (A∪B = U). Докажем, что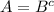
Доказательство. Пусть x∈A, при этом возможны два варианта:
x∈B или x∉B, то есть x∈B или x∈.
Если x∈B, тогда имеем x∈A∩B = ∅⊂
либо же x∈ и x∈A, ⇔ x∈A∩ ⊂,
то есть если x∈A => x∈
Пусть x∈, тогда x∈U\B, что значит x∈U и x∉B,
но т.к. U = A∪B, то имеем x∈A∪B и x∉B, то есть имеем
(x∈A или x∈B) и x∉B
если x∈A и x∉B, ⇔ x∈A\B ⊂ A, => x∈A,
если же x∈B и x∉B, то x∈∅ ⊂A, то есть x∈A,
итак ⊂A.
Мы доказали, что A⊂, и
.
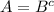чтд.
24и кратным 6,
Делитель это число на которое делится данное число.
24:2=12; 24:12=2. и 2 и 12 делители просто делим от 1 до самого числа на все что делится
24:1=24; 24:2=12; 24:3=8; 24:4=6; 24:6= 4; 24:8=3; 24:12=2; 24:24=1.
Делители 24-- (1;2;3;4;6;8;12;24)
Кратные 6 --(24;12;6;)
Кратное числу, это число которое делится на данное число умножаем подряд на 1,2,3.. Само число и ответ это кратное числу.
6•1=6; 6•2=12; 6•3=18; 6•4=24 ; дальше не подходят (6•5=30 больше чем 24).
6;12;18;24 кратны 6; но мы выбираем те, что будут делателями 24,
24:18 =не делится нацело, не подходит.
Совпадают 6;12;24.
ответ:
Делителем 24 и кратным 6 являются числа 6; 12; 24.
36 и кратным 9,
36:1=36; 36:2=18; 36:3=12; 36:4=9; 36:6=6; 36:9=4; 36:12=3; 36:18=2; 36:36=1;
делители 36 (1;2; 3;4;6;9;12;18;36).
Кратны 9.
9•1=9; 9•2=18; 9•3=27; 9•4=36.
Совпадают 9;18;36.
ответ: делителем 36 и кратными 9 являются числа 9;18;36.
100 и кратным 20,
100:1=100; 100:2=50; 100:4=25; 100:5=20; 100:10=10; 100:20=5; 100:25=4; 100:50=2; 100:100=1.
Делители 100 (1;2;4;5;10;20;25;50;100).
Кратные 20.
20•1=20; 20•2=40; 20•3=60; 20•4=80; 20•5=100.
Совпадают 20;100.
ответ: делителем 100 и кратные 20 являются сами числа 20 и 100.
108 и кратным 36
108:1=108; 108:2=54; 108:3=36; 108:4=27; 108:6=18; 108:9=12; 108:12=9; 108:18=6; 108:36=3; 108:54=2; 108:108=1
Делители 108 (1;2;3;4;6;9;12;18;36;54;108)
Кратные 36.
1•36=36; 2•36=72; 3•36=108.
Совпадают (36;108)
ответ: делителем 108 и кратными 36 являются сами числа 36 и 108.