у = 8/9.
Пошаговое объяснение:
Сумма числа 4 и выражения 3у - 0,5 равна 4 + (3у - 0,5).
Их произведение равно 4 • (3у - 0,5).
Зная, что сумма меньше произведения на 2,5, составим уравнение:
4 • (3у - 0,5) - (4 + (3у - 0,5)) = 2,5
12у - 2 - 4 - 3у + 0,5 = 2,5
12у - 3у = 2,5 + 6 - 0,5
9у = 8
у = 8/9
ответ: 8/9.
Проверим результат:
Сумма числа 4 и выражения 3у - 0,5 равна 4 + 3•8/9 - 1/2 = 3 1/2 + 2 2/3 = 3 3/6 + 2 4/6 = 5 7/6 = 6 1/6.
Их произведение равно 4 • (3•8/9 - 0,5) = 32/3 - 2 = 10 2/3 - 2 = 8 2/3.
Найдём, на сколько произведение больше, чем сумма:
8 2/3 - 6 1/6 = 8 4/6 - 6 1/6 = 2 3/6 = 2 1/2 = 2,5. ответ верный.
Найдем сначала наибольшее и наименьшее значения функции
y=(x+1)²(5-x). В силу того, что функция извлечения корня третьей степени монотонно возрастает, достаточно будет затем умножить найденные значения на 2, извлечь корень третьей степени из получившихся чисел, после чего вычесть из них 2.
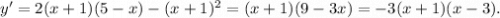
Внутри интервала (-3;3) лежит один из нулей производной - это x=-1. Найдем значения функции в точках -3; 3 (концах отрезка) и в точке -1:
y(-3)=y(3)=32 - наибольшее значение; y(-1)=0 - наименьшее значение.
Осталось с получившимися числами проделать указанные операции - умножить на 2, извлечь корень третьей степени и вычесть 2:
![\sqrt[3]{2\cdot 32}-2=4-2=2;\ \sqrt[3]{2\cdot 0}-2=-2.](/tpl/images/2074/3094/1128c.png)
ответ: наибольшее значение равно 2 и достигается на концах отрезка, наименьшее значение равно минус 2 и достигается в точке минус 1.