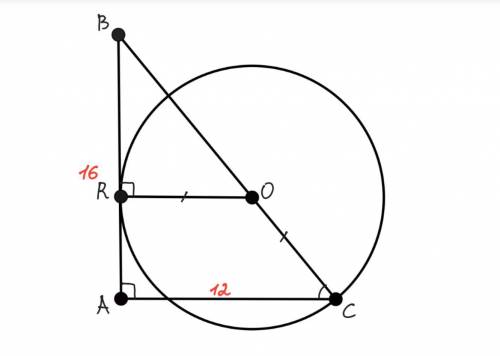
Дано: ΔABC — прямокутний, АВ і АС — катети, АВ=16 см, АС=12 см, коло(R;OC), т.О∈ВС, т.R — точка дотику кола до ΔАВС, т.R∈AB.
Знайти: радіус R кола.
Розв'язання.
1) Знайдемо гіпотенузу ВС ΔАВС за т.Піфагора:
АВ²+АС²=ВС²;
16²+12²=ВС²;
ВС²= 256+144;
ВС²= 400;
ВС= 20 см (–20 не задовольняє умові)
2) Проведемо радіус OR. R=OR=OC. Оскільки т.R — точка дотику, то OR⟂АВ.
3) Оскільки OR⟂AB і AB⟂AC (катети перпендикулярні), то OR||AC і трикутники ΔАВС і ΔRBO подібні за лемою.
(Лема про подібні трикутники: пряма, паралельна стороні трикутника, відтинає від нього трикутник, подібний даному)
4) ΔАВС подібний ΔRBO. Це означає, що відповідні сторони цих трикутників відносяться.
А тому справедливою буде така рівність:
АС/OR=BC/BO.
Нехай OR=OC=R (радіус, який потрібно знайти). Тоді ВО=ВС–ОС=ВС–R=20–R.
AC / R=BC / (BC–R);
12 / R= 20 / (20–R); (по пропорции решаем)
12(20–R)=20R;
240–12R=20R;
240=32R;
R= 240/32;
R= 15/2;
R= 7,5 (см)
Відповідь: 7,5 см.
ответ Б.
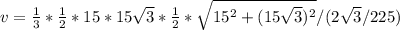
Пошаговое объяснение:
ДАНО: ПИРАМИДА
ΔАВС- прямоугольный
АВ=15, ВС=15√3
∠a =arctg(2√3)/225
НАЙТИ: Vпирамиды
V= 1/3 Sосн*h
1) ΔABC прямоугольный AB, BC катеты, Sосн=1/2*AB*BC
2) Высота пирамиды "h", опущенная из вершины D, в точку "0", причем "0" является точкой центром описанной окружности ΔАВС, то есть, точкой пересечения срединных перпендикуляров, проведенных к сторонам ΔАВС.(в часном случае ΔАВС прямоугольный, и "О" лежит на гипотенузе АС )
Δ ΔОЕВ - прямоугольный , с катетами "ОЕ" "ОМ" и дпины их равны половине соответствующих катетов ΔАВС OB²=OE²+OM²=1/4(AB²+BC²)
Из ΔDBO Прямоугольный, известен катет и прилежащий угол,
∠a нам дан. tg∠a= OE/OB OE=OB/tg∠a
рабочая формула будет иметь вид
V=1/3 *1/2*AB*BC* h 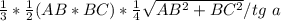
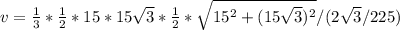
как то так
калькулятор в
