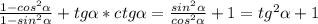
Пусть M и N – середины рёбер BC и AC данной пирамиды ABCD , все рёбра которой равны a . Тогда MN – средняя линия треугольника ABC . Поэтому MN || AB . Значит, угол между скрещивающимися прямыми DM и AB равен углу между пересекающимися прямыми DM и MN . Так как DM и DN – высоты и медианы равносторонних треугольников BCD и ACD , то
DN = DM = BD sin DBM = BD sin 60o = .
Кроме того, MN = AB = . Пусть K – середина MN . Тогда DK – медиана и высота равнобедренного треугольника DMN . Следовательно,
cos DMN = = = = .
ответ
arccos
(1-cos²a)/(1-sin²a) +tga*ctga= (sin²a+cos²a-cos²a)/(sin²a+cos²a-sin²a) + 1= sin²a/cos²a+1=tg²a+1
формулы использованные в решении
1=sin²a+cos²a
tga*ctga=1
ответ
tg²a+1