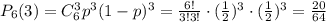Пошаговое объяснение:
Предположим, что им осталось проехать 1 часть пути.
По условию эта часть в 4 раза меньше, чем они уже проехали, т.е. проехали они в 4 раза больше:
1ч * 4 = 4 части пути они проехали.
Тогда весь путь составляет: 1ч + 4ч = 5ч.
Но мы знаем, что путь равен 60 км, следовательно, 1ч. будет составлять:
60км : 5ч = 12км - 1 часть
Но 1ч - тот путь, что им осталось проехать, т.е 12км.
Значит, проехали они:
60 - 12 =48 (км)
Или по другому:
1ч = 12км , а 4ч. = 4 *12 =48 (км) - проехали до заправки

a)
Испытание состоит в том, что из (5+12+9)=26 шаров извлекают два
n=C²₂₆=26!/(2!·24!)=(25·26)/2=325
событие A-"два шара синего или зелёного цвета"
m=C²₅+C²₁₂=(5!/(2!3!)) + (12!/(2!10!))=10+66=76
p(A)=m/n=76/325
б)
(12/26) -Вероятность того, что первый шар зеленый
После этого шаров 25, зеленых там 11
(11/25) -Вероятность того, что второй шар зеленый
(10/24) -Вероятность того, что третий шар зеленый
По теореме умножения:
p=(12/26)·(11/25)·(10/24)=11/130 - вероятность того, что все три шара будут только зелёного цвета.
Аналогично
p=(5/26)·(12/25)·(9/24)+(12/26)·(5/25)·(9/24)+(9/26)·(12/25)·(5/24)+
+(5/26)·(9/25)·(12/24)+(12/26)·(9/25)·(5/24)+(9/26)·(5/25)·(12/24)=
=6·(9/26)·(12/25)·(5/24)=27/130- вероятность того, что шары будут разных цветов
2.
a)
событие A-"не все выстрелы дадут перелёты"
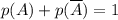
Находим вероятность противоположного события
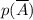 =(1/2)·(1/2)·(1/2)·(1/2)·(1/2)·(1/2)=1/64 - вероятность того, что все выстрелы дадут перелёты.
=(1/2)·(1/2)·(1/2)·(1/2)·(1/2)·(1/2)=1/64 - вероятность того, что все выстрелы дадут перелёты.

б) По формуле Бернулли: