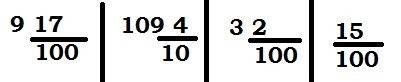
ответ: градусная мера угла СВD равна 50 градусов, градусная мера угла АВD равна 130 градусов.
Пошаговое объяснение:
Из условия известно, что луч BD делит развернутый угол АВС на два угла, градусная мера угла АВD в 2.6 раза больше градусной меры угла CBD. Для начала вычислим с уравнение градусную меру угла CBD.
Пусть х - градусная мера угла CBD.
Пусть 2.6х - градусная мера угла АВD.
Развернутый угол всегда равен 180 градусов.
Составим и решим уравнение.
х + 2.6х = 180;
3.6х = 180;
х = 180 : 3.6;
х = 50 (градусов) - угол СВD.
Теперь можем вычислить градусную меру угла АВD.
50 * 2.6 = 130 (градусов) - угол АВD.
288√3 cм³
Пошаговое объяснение:
Правильная пирамида – это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания. Апофема – это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания. Апофемы всех боковых граней правильная пирамиды равны.
Объём пирамиды через площадь основания S и высоту H определяется по формуле:
V = S•H/3.
По условию основание правильной пирамиды – четырехугольник. Тогда, по определению правильной пирамиды, основание – квадрат со стороной a=12 см. Тогда площадь основания S=a²=(12 см)² =144 см².
Точку пересечения диагоналей основания обозначим О, вершину пирамиды – K (см. рисунок):
ОK - высота пирамиды, KM - апофема боковой грани ΔAKB.
Так как DA=12 см, то ОМ=DA:2=12:2 см = 6 см.
Так как ΔОKM прямоугольный с ∠KОМ=90° и по условию ∠ОKM=30°, то по определению
ctg30°= ОK/ОМ.
Отсюда ОK=ОМ•ctg30°=6 см•√3=6√3 см.
Тогда объем пирамиды равен
V=(144•6√3)/3=288√3 cм³.

109,4 = 109 4/10 = 1094/10 = 547/5,
3,02 = 3 2/100 = 302/100 = 151/50,
0,15 = 15/100 = 3/20