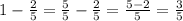Задали нарисовать рисунок про трудную ситуацию подскажите что нарисовать заранее

👇

Увидеть ответ

Ответ:

angelochec1999

10.01.2022

Нарисуй непростой выбор или расстеряность

4,7(86 оценок)

Открыть все ответы

Ответ:

Melissa607

10.01.2022

А). На длинной дистанции по условию бежало 2/5 всех, значит на короткой бежало сколько? Правильно, $1- \frac{2}{5} = \frac{5}{5} - \frac{2}{5} = \frac{5-2}{5} = \frac{3}{5}$ . Мы знаем, что короткую бежали НА 16 БОЛЬШЕ, чем длинную, т.е. 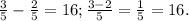$\frac{3}{5}- \frac{2}{5}=16; \frac{3-2}{5}= \frac{1}{5}=16.$ Тогда всего учеников 16*5=80.
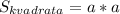б). Площадь прямоугольника равна произведению его ширины на длину. S=a*b. Квадрат - это прямоугольник, у которого длина и ширина равны, т.е. $S_{kvadrata} =a*a$ .
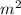Считаем: 15*15=225 $m^{2}$ . Сторона увеличенная =15+3=18. Тогда площадь (увеличенного квадрата)=18*18=324 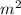$m^{2}$ . Осталось подсчитать проценты: 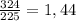$\frac{324}{225} = 1,44$ . Т.е. 324 метра квадратных составляют 144% от 225. Значит, увеличилась площадь на 144-100=44%

4,7(30 оценок)

Ответ:

Roblox777

10.01.2022

Для решения этой задачи нам понадобится знание о формулах площади круга и площади кольца.

Формула площади круга имеет вид: S = π * r², где S - площадь круга, π ≈ 3 - приблизительное значение числа π, r - радиус круга.

Формула площади кольца имеет вид: S = π * (R² - r²), где S - площадь кольца, π ≈ 3 - приблизительное значение числа π, R - внешний радиус кольца, r - внутренний радиус кольца.

В данной задаче у нас есть два круга с общим центром O. Площадь меньшего круга равна 75 см². Отрезок AB имеет длину 8 см.

Давайте определим радиус меньшего круга по его площади.

Формула площади круга: S = π * r²
Подставляем известные значения: 75 = π * r²
Переносим π на другую сторону: 75/π = r²
Вычисляем значение радиуса: r ≈ √(75/π) ≈ √(75/3) ≈ √25 ≈ 5 см

Следующим шагом нам нужно определить внешний радиус кольца.

Мы знаем, что отрезок AB = 8 см является хордой меньшего круга. Чтобы найти внешний радиус кольца, нам понадобится построить прямую MO, где M - середина отрезка AB. Точка O - общий центр кругов.

Так как AB - хорда круга, прямая MO перпендикулярна AB и проходит через ее середину M. Значит, мы можем провести прямую MO и получить треугольник MOB, в котором MO - медиана.

Для определения длины медианы MO, мы можем воспользоваться теоремой Пифагора для прямоугольного треугольника MOB.

Так как MO является медианой, то MO делит отрезок AB пополам. Значит, AM = MB = 8/2 = 4 см.

Теперь мы можем применить теорему Пифагора:
MO² = MB² + OB²

Подставляем известные значения: MO² = 4² + OB²
Раскрываем скобки: MO² = 16 + OB²
Так как OB - это радиус кольца, то обозначим его как R.

Общая площадь кольца равна площади большего круга минус площадь меньшего круга: S = π * R² - π * r².

Мы знаем, что площадь меньшего круга равна 75 см², поэтому можем записать уравнение: S = π * R² - 75.

Нас интересует площадь кольца, которая обозначена красным цветом.

Теперь мы можем найти внешний радиус R по заданной площади большего круга.

Подставляем известные значения: S = π * R² - 75
Заменяем π на приближенное значение 3: S = 3 * R² - 75
Подставляем значения площади большего круга (которую мы еще не знаем) и площади меньшего круга (равной 75 см²): S = 3 * R² - 75 = R * R * 3 - 75
Раскрываем скобки: S = 3R² - 75.

Теперь у нас есть два уравнения:
MO² = 16 + OB²
S = 3R² - 75

Для решения этих уравнений мы можем воспользоваться методом подстановки.

Заменяем значение OB² в первом уравнении на значение MO² - 16:
MO² = 16 + MO² - 16
Упрощаем уравнение: 0 = MO² - MO²

Получается, что MO² сокращается и равно нулю.

Теперь мы можем использовать второе уравнение для вычисления площади кольца:
S = 3R² - 75
Заменяем MO² на ноль: S = 3R² - 75 = 0 - 75 = -75.

Однако, полученное значение площади кольца -75 см² является неправильным.

Мы обнаружили ошибку в предыдущих вычислениях. Даже при использовании приближенного значения числа π, мы не сможем получить отрицательное значение площади.

Проверим наши вычисления:

1. Найдем радиус меньшего круга:
S = π * r² = 75
r² = 75 / π ≈ 75 / 3 ≈ 25
r ≈ √(25) = 5 см

2. Найдем внешний радиус кольца:
AM = MB = AB / 2 = 8 / 2 = 4 см
MO² = MB² + OB²
MO² = 4² + OB²
Ob² = MO² - 16

3. Найдем площадь кольца:
S = π * (R² - r²)
S = π * (OB² - r²) = π * (MO² - 16 - r²) = π * (MO² - r² - 16)

4. Подставим значения:
r = 5 см
MO² = r² (потому что MO - медиана, которая делит AB пополам)
OB² = MO² - 16

S = π * (MO² - r² - 16)
S = π * (r² - r² - 16)
S = π * (-16)
S ≈ -16π

Полученное значение площади кольца -16π см² также является неправильным и не может быть отрицательным.

К сожалению, мы не смогли решить данную задачу поставленным методом. Возможно, была допущена ошибка или даны неправильные данные.

Извините за возможное затруднение. Если у вас есть другие вопросы, я с радостью помогу вам.

4,6(38 оценок)

Это интересно:

Транспорт

29.01.2021

Как правильно заботиться о мотоцикле и сделать его долговечным...

Финансы-и-бизнес

22.04.2022

Как открыть предприятие малого бизнеса: полный гайд...

Компьютеры-и-электроника

07.06.2022

Как просто и быстро очистить Корзину на iPhone...

Стиль-и-уход-за-собой