N=2 P=1/2
N=3 P=3/8
N=4 P=3/8
Пошаговое объяснение:
Если человек собирается сдать деньги будем обозначать его как 1, если собирается забрать, то (-1). Таким образом очередь в банк можно изобразить как строку из 1 и -1 длины n. Всего возможных комбинаций
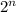 . Для n=2 это следующие строки
. Для n=2 это следующие строки
Не остановится
1 1 (сумма 2)
1 -1 (сумма 0)
Остановится ( всего 2)
-1 1
-1 -1
Будем складывать цифры в нашей очереди, начиная с самого левого.
Если на каком-то шаге получается отрицательное число, то это говорит о том, что очередь остановится. Для n=2 таких вариантов 2, в остальных случаях (4-2) очередь не остановится и вероятность данного события 2/4=1/2.
Для следующего решения разобьем все найденные варианты на группы Остановится и Не остановится. Для вариантов из группы Не остановится вычислим сумму цифр.
Для n=3 количество вариантов 8. Каждый из них получается приписыванием к вариантам на предыдущем ходе 1 или -1.
При этом все варианты из группы Остановится остаются в этой группе независимо от приписываемой цифры и их количество удваивается, для остальных случаев результат зависит от исходной суммы.
Распишем во что перейдут существующие группы:
Cумма 2 (кол-во 1) => Cумма 3 (кол-во 1) , Cумма 1 (кол-во 1)
Cумма 0 (кол-во 1) => Cумма 1 (кол-во 1) , Cумма -1 (кол-во 1)
Мы получим следующую картину:
Не остановится
Cумма 3 (кол-во 1)
Cумма 1 (кол-во 2)
Остановится ( всего 2*2+1=5)
Вероятность искомого события 3/8
Для n=4 получается следующее разбиение
Не остановится
Cумма 4 (кол-во 1)
Cумма 2 (кол-во 3)
Cумма 0 (кол-во 2)
Остановится ( всего 5*2=10)
Вероятность искомого события 6/16=3/8
ответ:arctg(3+√73)/4+nπ, arctg(3-√73)/4+nπ,где n∈Z ; arctg(3+√73/)/4
Пошаговое объяснение:2sin²x-3sinxcosx-8cos² x=0 Это уравнение однородное, второй степени. Разделим обе части уравнения на Cos²x≠0, т.е. х≠π/2+nπ, где n∈Z. Тогда получим уравнение: 2tg²x-3tgx-8=0. Пусть tgx=y ⇒2y²-3y-8=0, дискриминант D= 9+64=73 Значит у₁= (3+√73)/4; у₂=(3-√73)/4 Поэтому tgx=(3±√73)/4 ⇒ x₁=arctg(3+√73)/4+nπ, x₂=arctg(3-√73)/4+nπгде n∈Z .
По условию 0≤х≤π/2, значит отберём корни уравнения с неравенства: 0≤arctg(3±√73)/4+nπ ≤π/2
По определению арктангенса имеем, что -π/2<arctga<π/2
1) 0 < arctg(3+√73)/4<π/2
2) arctg(3-√73)/4=-arctg(√73-3)/4⇒ -π/2<arctg(3-√73)/4<0
если n=1, то корни не принадлежат [0;π/2]: 0+π≤arctg(3+√73/)/4+π<π/2+π
-π/2+π<arctg(3-√73)/4<0+π
если n= -1, то корни не принадлежат [0;π/2]: 0-π≤arctg(3+√73/)/4-π<π/2-π
-π/2-π<arctg(3-√73)/4-π <0-π
если n=0, то корни принадлежат [0;π/2]: 0≤arctg(3+√73/)/4+0<π/2
корень arctg(3+√73/)/4 принадлежит [0;π/2]
24:6=4 км/ч пешеход
2)280: 40 = за 7 часов теплоход км
350:7=50 км/ч скорость автобуса
Первые два щас еще напишу.