y = C1 e‾ᵡ + C2 x e‾ᵡ + x^2 -4x +10
Пошаговое объяснение:
y'' + 2y' + y = x^2 + 4
однородное уравнение имеет вид
y'' + 2y' + y = 0
составим соответствующее характеристическое уравнение
k^2 + 2k + 1 = 0
(k+1)^2 = 0
k+1 =0 > k1,2 = -1
имеем два действительных кратных корня
Общее решение однородного уравнения
yo = C1 e‾ᵡ + C2 x e‾ᵡ
Частное решение ищем в виде
yч = Ax^3 +Bx^2 +Cx +D
находим производные
yч' = (Ax^3 +Bx^2 +Cx +D)' =3Ax^2 +2Bx +C
yч" = (3Ax^2 +2Bx +C)' = 6Ax +2B
подставляем в исходное уравнение
yч'' + 2yч' + yч = 6Ax +2B + 2 (3Ax^2 +2Bx +C) + Ax^3 +Bx^2 +Cx +D =
= Ax^3 +(6A+B)x^2 + (6A+4B+C)x + (2B+2C+D) = x^2 +4
Решаем систему из соответствующих коэффициентов
x^3: A = 0
x^2: 6A+B = 1; B = 1-6A = 1-6*0 = 1
x^1: 6A+4B+C = 0; C = -6A -4B = -6*0 -4*1 = -4
x^0: 2B+2C+D = 4; D = -2B -2C = 4 -2*1 -2*(-4) =10
Частное решение имеет вид
yч = 0*x^3 + 1*x^2 -4x +10 = x^2 -4x +10
Общее решение линейного неоднородного дифференциального уравнения
y = yo + yч = C1 e‾ᵡ + C2 x e‾ᵡ + x^2 -4x +10
Задание 2
Составьте простой план и напишите текст (объем письменной работы 100-150 слов) на одну из предложенных тем. В письменную работу включите предложения с прямой речью.
1. Придумайте и напишите сказку для младших школьников о том, как появился первый космический корабль.
2. Напишите письмо своему другу (подруге), в котором пригласите его (ее) совместно посетить выставку современных автомобилей. Расскажите в письме о том, какие автомобили будут представлены на выставке.
3. Представьте, что вы участник праздника «День языков народа Казахстана». Напишите в своем дневнике, что происходило в этот день. Постарайтесь передать ваши чувства, эмоции, настроение.
4. Напишите рекламный текст для учащихся об открытии «Школы иностранных языков». Постарайтесь убедить школьников записаться в школу и обязательно посещать занятия.
300 м² + 2 га < 600 а : 2
[1 га = 10 000 м²
2 га = 2 * 10 000 = 20 000 м²
300 м² + 2 га = 300 м² + 20 000 м² = 20 300 м²
600 а : 2 = 300 ар [1 ар = 100 м²]
300 ар = 300 * 100 = 30 000 м²
2 см³ - 100 мм³ > 1 дм³ - 200 см²
[1 см = 10 мм]
[1 см³ = 1 см * 1 см * 1 см = 10 мм * 10 мм * 10 мм = 1000 мм³]
2 см³ = 2 * 1000 = 2000 мм³
2 см³ - 100 мм³ = 2000 мм³ - 100 мм³ = 1900 мм³
[1 дм = 10 см]
[1 дм³ = 1 дм * 1 дм * 1 дм = 10 см * 10 см * 10 см = 1000 см³]
1 дм³ - 200 см³ = 1000 см³ - 200 см³ = 800 см³
1000 см³ - 1 дм³ < 800 м² : 4 м
[1 дм = 10 см]
[1 дм³ = 1 дм * 1 дм * 1 дм = 10 см * 10 см * 10 см = 1000 см³]
1000 см³ - 1 дм³ = 1000 см³ - 1000 см³ = 0
800 м² : 4 м = 200 м
2000 дм³ + 200 м³ > 200 см³ + 2000 см³
[1 м = 10 дм]
[1 м³ = 1 м * 1 м * 1 м = 10 дм * 10 дм * 10 дм = 1000 дм³]
200 м³ = 200 * 1000 = 200 000 дм³
2000 дм³ + 200 м³ = 2000 дм³ + 200 000 дм³ = 202 000 дм³
200 см³ + 2000 см³ = 2200 см³
[1 дм = 10 см]
[1дм³ = 1 дм * 1 дм * 1 дм = 10 см * 10 см * 10 см = 1000 см³]
202 000 дм³ = 202 000 * 1000 = 202 000 000 см³
Найдем начала общее решение соответствующего однородного дифференциального уравнения
Воспользовавшись заменой Эйлера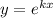 , мы получим характеристическое уравнение
, мы получим характеристическое уравнение
Общее решение уравнения (*)
Далее нужно найти частное решение. Рассмотрим функцию:
Здесь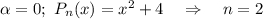
Сравнивая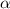 с корнями характеристического уравнения и, принимая во внимая, что
с корнями характеристического уравнения и, принимая во внимая, что 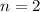 частное решение будем искать в виде
частное решение будем искать в виде
Подставляем все это в исходное дифференциальное уравнение
Приравниваем коэффициенты при степени x
Частное решение: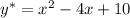
Общее решение линейного неоднородного дифференциального уравнения: