36 легковых машин
Пошаговое объяснение:
240 машин - 100%, или же все машины в автопарке;
x грузовых = 60% из всех;
y легковых - 25% из грузовых.
Сперва найдём кол-во грузовых машин x с пропорции:
240 - 100%
х - 60%
х = (240 * 60) / 100 = 144 (грузовых машин).
Теперь, зная кол-во грузовиков, можем найти кол-во легковых машин, так как их кол-во связанно с кол-вом грузовых. Примем все грузовые как 100%. Опять же по пропорции:
144 грузовых - 100%, или же все грузовые;
у легковых - 25% из грузовых;
у = (144 * 25) / 100 = 36 (легковых машин).
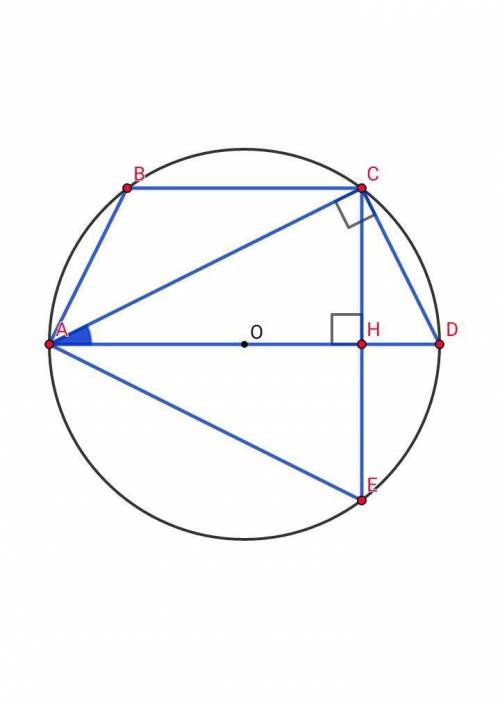
Диагональ равнобокой трапеции перпендикулярна боковой стороне и образует с основанием трапеции угол α. Найдите высоту трапеции, если радиус окружности, описанной около трапеции, равен h.
=============================================================
Первый Около равнобедренной трапеции всегда можно описать окружность. С учётом условия (∠АСD = 90°) получаем, что АD - диаметр описанной окружности. AD = 2h.Если вписанный в окружность угол прямой, то он опирается на диаметр этой окружности.Продолжим высоту СН трапеции до пересечения с описанной окружностью в точке Е. Диаметр окружности является серединным перпендикуляром по отношению к хорде СЕ ⇒ СН = НЕ, AD⊥CE ⇒ ΔACE - равнобедренный, АС = АЕ, ∠CAD = ∠EAD = α, ∠САЕ = 2α. Или можно ссылаться на симметрию относительно AD.По теореме синусов: R = h = CE/2•sin2α = 2•CH/2•sin2α = CH/sin2α ⇒ CH = h•sin2αВторой В ΔACD: cosα = AC/AD ⇒ AC = AD•cosα = 2h•cosαВ ΔАСН: sinα = CH/AC ⇒ CH = AC•sinαЗначит, СН = (2h•cosα) •sinα = h•sin2αОТВЕТ: h•sin2α