— неоднородное дифференциальное уравнение третьего порядка с постоянными коэффициентами
Принцип суперпозиции решений
Общее решение такого уравнения: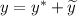 
, где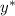 
— общее решение соответствующего однородного уравнения, 
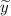— частное решение неоднородного дифференциального уравнения с постоянными коэффициентами.
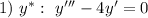
Метод Эйлера: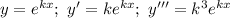 
Характеристическое уравнение: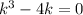 
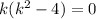
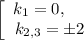
Фундаментальная система решений:
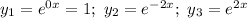
Общее решение: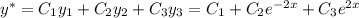 
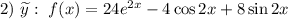
Здесь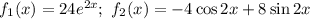 
Контрольные числа: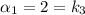 
— является корнем характеристического уравнения; 
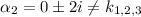— не является корнем характеристического уравнения;
Тогда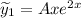 
и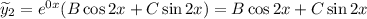 
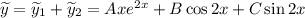
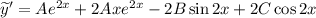
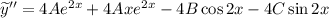
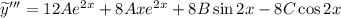
Находим неизвестные коэффициенты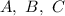 
методом неопределенных коэффициентов:
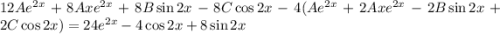
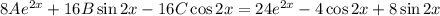
Коэффициенты около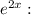 
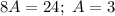
Коэффициенты около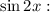 
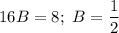
Коэффициенты около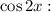 
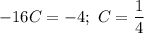
Таким образом,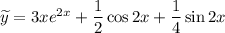 
Общее решение заданного уравнения:
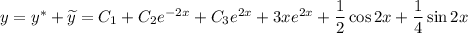
ответ: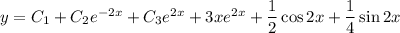 
1)
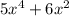
2)
функция - не монотонная
экстремумы: (-6; 540), (8; -832)
3)
минимум f(4)= -1
максимум f(2)=3
Пошаговое объяснение:
1)
просто диференцируем по частям
2)
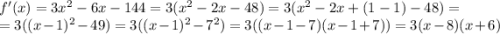
это производная исходной функции
как бы тут уже видно, что производная:
квадратичная парабола,
роги вверх,
знак меняет (а это значит, что исходная функция - не монотонная) в точках: x1 = -6; x2 = 8. это и будут точки экстремумов
минимум и максимум производной нас не интересуют
Решаем уравнение
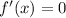
3(x-8)(x+6) = 0
x1 = -6
x2 = 8
y1 = 540 = (-6)³ -3*(-6)² - 144*(-6) = -216 -108 + 864 = -324 + 864 = 540
y2 = -832 = 8³ -3*8² -144*8 = 8*64 - 3*64 - 144*8 = 5*8*8 - 144*8 =
= 8*(40-144) = 8*(-104) = -800 -32= -832
3)
f(2) = 4-16+15 = 3
f(5) = 25 -40 +15 =0
f'(x) = 2x-8
f'(x) = 0 при х = 4
f(4) = 16 - 32 +15 = -1
из f(2)=3, f(4)= -1, f(5)=0 выбираем минимум и максимум
минимум f(4)= -1
максимум f(2)=3
прим.: на втором таки уткнулся. противно его считать в голове. по быстрому там тупо решается квадратное уравнение через дискриминант на листике
