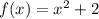 определена на множестве E
определена на множестве E 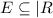
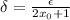 где
где 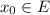 .
. на области
на области 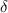 от
от  (то есть:
(то есть: 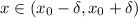 ) выполняется
) выполняется 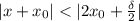 .
.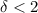 , выполняется
, выполняется 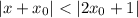 .
.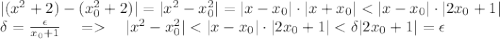
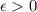 есть
есть 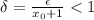 , на области которой выполняется
, на области которой выполняется 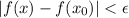
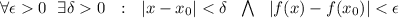 ). Следовательно -
). Следовательно - 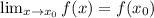 .
.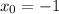 нужно отдельно доказать предел
нужно отдельно доказать предел 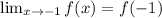 .
. . Но! Множество натуральных чисел
. Но! Множество натуральных чисел 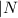 тоже подмножество
тоже подмножество  , значит
, значит 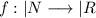 тоже непрерывна, получается - доказали что
тоже непрерывна, получается - доказали что 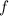 непрерывна на области определения? Известно, что
непрерывна на области определения? Известно, что 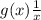 тоже непрерывна на области определения, но
тоже непрерывна на области определения, но 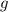 , понятное дело, не определена на
, понятное дело, не определена на  !
! " или, "непрерывна на отрезке
" или, "непрерывна на отрезке 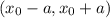 "...
"...1 a
2 a
3 ә
4б
5в
6в
7а
8 жолдас товарищ
қарындас мл.сестра
тату дружный
немере внук, внучка
аға ст.брат
іні мл.брат
жиен племянник
танысу знакомство
жақын близкий, родной
дәстүр традиция, обычай
Пошаговое объяснение:
2 задание
От-ба-сы-мыз 4буын, 9әріп, 9дыбыс
о-дауысты, жуан, ашық, еріндік
т-дауыссыз, қатаң
б-дауыссыз үнді
а-дауысты, ашық, жуан, езулік
с-дауыссыз, қатаң
ы-дауысты, жуан, қысаң, езулік
м-дауыссыз үнді
ы-дауысты, жуан, қысаң, езулік
з- дауыссыз, ұяң
шө-бе-ре-сі 4 буын 8әріп 8дыбыс
ш-дауыссыз, қатаң
ө-дауысты, жіңішке, ашық, еріндік
б-дауыссыз, ұяң
е-дауысты, ашық, жіңішке, езулік
р-дауыссыз, үнді
е-
с-дауыссыз, қатаң
і-дауысты, жіңішке, қысаң, езулік
мү ше ле рі 4буын 8әріп 8дыбыс
м-дауыссыз, үнді
ү-дауысты, жіңішке, қысаң, еріндік
ш-дауыссыз қатаң
е-
л-дауыссыз үнді
е-
р-дауыссыз, үнді
і-
3.О-қу-шы-лар
о, қу, шы-ашық буындар
лар-бітеу буын
ә-кем
ә -ашық буын
кем -бітеу буын
а-ғам-ның
а-ашық буын
ғам, ның - бітеу буындар
дәс-түр-лер
барлығы бітеу буын
от-ба-сы-мыз-дың
от-тұйық буын
ба, сы - ашық
мыз, дың -бітеу буындар
Всё