ответ: b = (-3,6,6), b (3; -6; -6), α = -60⁰
Пошаговое объяснение:
Дан вектор a(-1;2;2). Найдите координаты вектора b, коллинеарного вектору a, если a·b = 27.
Скалярное произведение векторов а и b определяется как произведение длин этих векторов на косинус угла между ними!
Поскольку векторы коллинеарные, то угол между ними равен 0 градусов, т. е косинус угла равен 1.
Длина вектора a равна
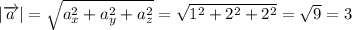
По условию задания скалярное произведение векторов равно 27
Зная длину вектора а найдем длину вектора b
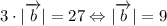
Поскольку вектора а и b коллинеарны, то и координаты связаны уравнением
Подставим координаты вектора а
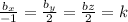
Запишем координаты вектора b через новую переменную k bx = -k, by =2k, bz = 2k
b = (-k,2k,2k)
Определим длину вектора и по теореме Пифагора
Так как длину вектора b мы знаем из скалярного произведения то
3|k| = 9
k₁ = 3 k₂=-3
Получили два варианта вектора b
Для k = 3
b = (-3,6,6)
Для k = -3
b (3; -6; -6)
Найдем угол между векторами a и c из формулы скалярного произведения, если a*c = -6; c = 4
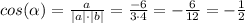
α = arccos(-0,5) = -60⁰
ответ: b = (-3,6,6), b (3; -6; -6), α = -60⁰
Пошаговое объяснение:
Дан вектор a(-1;2;2). Найдите координаты вектора b, коллинеарного вектору a, если a·b = 27.
Скалярное произведение векторов а и b определяется как произведение длин этих векторов на косинус угла между ними!
Поскольку векторы коллинеарные, то угол между ними равен 0 градусов, т. е косинус угла равен 1.
Длина вектора a равна
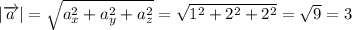
По условию задания скалярное произведение векторов равно 27
Зная длину вектора а найдем длину вектора b
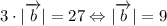
Поскольку вектора а и b коллинеарны, то и координаты связаны уравнением
Подставим координаты вектора а
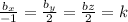
Запишем координаты вектора b через новую переменную k bx = -k, by =2k, bz = 2k
b = (-k,2k,2k)
Определим длину вектора и по теореме Пифагора
Так как длину вектора b мы знаем из скалярного произведения то
3|k| = 9
k₁ = 3 k₂=-3
Получили два варианта вектора b
Для k = 3
b = (-3,6,6)
Для k = -3
b (3; -6; -6)
Найдем угол между векторами a и c из формулы скалярного произведения, если a*c = -6; c = 4
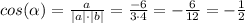
α = arccos(-0,5) = -60⁰
250 : 1000 = 0,25 (руб.) - цена 1 г дешёвых конфет
400 : 1000 = 0,4 (руб.) - цена 1 г дорогих конфет
Пусть купили х г дорогих конфет, тогда дешёвых купили (1000 - х) г.
За дорогие заплатили 0,4х руб., за дешёвые 0,25(1000 - х) руб.
Уравнение: 0,4х + 0,25(1000 - х) = 370
0,4х + 250 - 0,25х = 370
0,4х - 0,25х = 370 - 250
0,15х = 120
х = 120 : 0,15
х = 800 (г) - масса дорогих конфет
ответ: В 800 г.
Проверка:
0,4 * 800 + 0,25 * 200 = 370
320 + 50 = 370
370 = 370