f'(x) = -2sin2x + 6x
Пошаговое объяснение:
Квадрат я обозначу ^, т.к. ' - обычно знак производной.
Производная суммы равна сумме производных слагаемых. То есть f'(x) = (cos2x)' + (3x^2)' + (9)' .
Производная косинуса равна минус синус, при этом cos2x - сложная функция, для вычисления производной сложной функции нужно вычислить производную самой функции (-sin2x) и умножить на производную аргумента ((2x)'=2). Таким образом (cos2x)' = -2sin2x
Производная х^2 равна 2х (х^n=n*x^(n-1)). Производная произведения числа на переменную равна произведению числа и производной переменной. Таким образом (3x^2)' = 6х.
Производная числа равна 0.
Получаем f'(x) = (cos2x)' + (3x^2)' + (9)'
f'(x) = -2sin2x + 6x
1) ищем производную
2) приравниваем производную к нулю и ищем корни
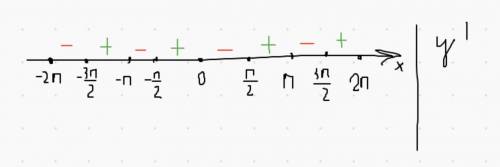
3) расставляем корни на прямой и смотрим, где функция возрастает/убывает и рассматриваем точки, где знак меняется с + на - и крайние точки.
Например, 1 :
y = cos(2x) + sin^2(x)
y' = cos'(2x) + (sin^2(x))' = -2sin(2x) + sin(2x) = -sin(2x)
y' = 0 <=> -sin(2x) = 0 <=> x = пk/2
рассмотрим значение каждой точки, переходящей с + на - :
y(-п) = 1
y(0) = 1
y(п) = 1
y(2п) = 1
Значит, наибольшее значение функции y=cos(2x)+sin^2(x) равно 1
ответ: 1
Дальше по аналогии, надеюсь, справишься)