1-ая задача:
На двух кубиках может выпасть либо четное, либо нечетное количество , значит выпадение четного числа 1 к 2-ум. На третьем кубике шанс выпадения 5-ти - 1 к шести (т.к. всего сторон у кубика шесть), значит общий шанс - 1/2 * 1/5 = 1/10.
2-ая задача:
0,93^6=0,64699018. Т.е. шанс примерно 65%.
3-я задача:
Судить можно следующим образом: Из 1-ой фабрики процент брака - 0,02, значит фактически в магазине 0,14 бракованных пальто. Аналогично со второй фабрикой. Получаем, что на второй фабрике 0,15 бракованных пальто. Всего пальто 11, значит процент брака на весь магазин составляет 0,29/11 = 29/1100, что равно 0,02636, что примерно равно 3%.
4-я задача:
Я не уверен, как решается эта задача, но, я думаю, что шанс падения на поле без линий составляет 5 к 9, ведь на каждые 9 см (расстояние от одной линии до другой учитывая поле касания монеты, при минимальном моприкосновении ее поверхности с линией) она будет падать в выигрушную позицию лишь в 5 см, что и составляет шнас 5 к 9.
5-я задача:
Из первой урны шанс вытащить синий шар составляет 1 к 3, когда из второй 1 к 2, значит вероятность вытащить два синих шара составляет 1 к 5. Аналогично с красными шарами вероятность вытащить красный шар из обоих урн составляет 1 к 9. Значит вероятность составляет 8 к 15.
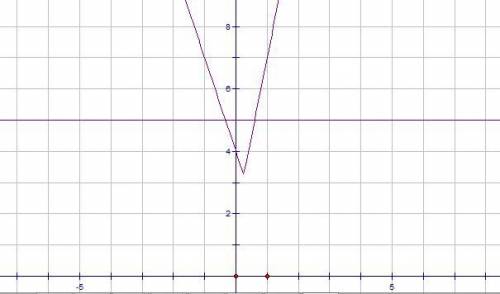
2)x=-0.8
3) x=-14
4) x=-13/18
5) x=7.9
6) x=-13/24