Через 0,8 ч они встретятся на расстоянии 3,2 км от города
Пошаговое объяснение:
Пусть х ч - проедет до встречи мотоциклист, тогда
( х+2,4)ч - проедет до встречи велосипедист.
46х км - проедет до встречи мотоциклист.
11,5*( х+2,4) км проедет до встречи велосипедист.
А по условию задачи эти расстояния равны
Составим ур-е:
46х=11,5*( х+2,4)
46х=11,5х+27,6
46х - 11,5х=27,6
34,5х=27,6
х=27,6:34,5
х=0,8 ч проедет до встречи мотоциклист
46*0,8=36,8 км - проедет до встречи мотоциклист
40-36,8=3,2 км - осталось доехать до города
ответ: оба по 9 часов
Пошаговое объяснение:
7)
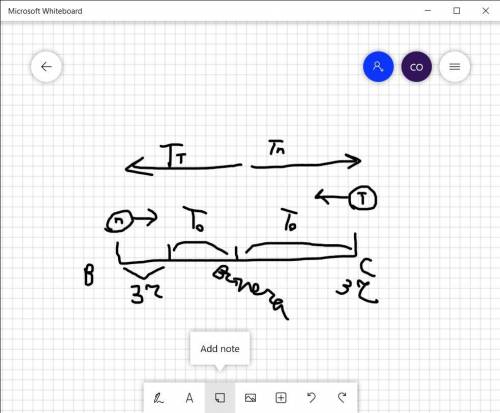
Итак, на рисунке немного запутанно, но потсараюсь объяснить:
п и т в кружочках--это пассажирский и товарный поезда. Сначала п ехал 3 часа сам, а потом навстречу ему начал ехать т. Псоле этого То времени, и они встретились. Затем Тт времени, чтоб т доехал до места назначения, а Тп, чтоб доехал п. Путь они проехали один и тот же. Выразим его через оба поезда
По условию известно, что Тп=3ч, а Тт=6 ч
Выразим путь через оба поезда
sп=(3+То+Тп)/vп
sт=(То+Тт)/vт
Приравниваем пути
(3+То+Тп)/vп=(То+Тт)/vт
(3+То+3)/vп=(То+6)/vт
(То+6)/vп=(То+6)/vт
Из этого следует, что Скорости у п и т равные.
А значит, в пути они находились равное количество часов
соотношение путей, которые они проехали после встречи
sот:sоп=Tот:Топ=6/3=2:1
Значит, соотношение путей до встречи будет 1:2 соответсвенно
т проехал 2/3 дороги за 6 часов (То+3), значит весь путь проехал за 9 часов
п проехал 1/3 дороги за 3 (То) часа, значит весь путь за 9 часов с начала движения
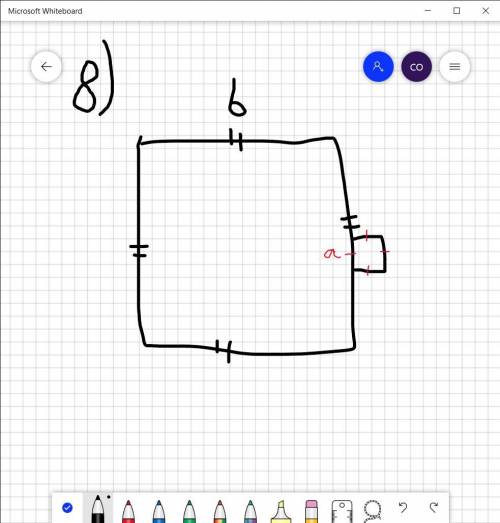
8) Обозначим сторону большого квадрата как Ь, а маленького-а
Таким образом периметр увеличился на 3а
Р1=Ро+3а=Ро*1.05
0.05Ро=3а
Ро=4Ь
0.05*4Ь=3а |:3
а=Ь*0.2/3
So=Ь^2
S1=b^2+a^2=b^2+(Ь*0.2/3 )^2=b^2+0.04b^2/9
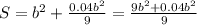
S1/So=((9,04b^2)/9)/b^2=9.04:9=1,00(4)
приблизительно увеличилось на 0,44%
Кузнечик делает 7 прыжков, значит k = 7. Всевозможные точки, в которых может оказаться кузнечик, описываются формулой : 7+2n, -k≤n≤0.
Эти точки: -7, -5, -3, -1, 1, 3, 5, 7.
Всего из k+1 = 7+1 = 8.
ответ: 8.
Теперь рассмотрим, сколько существует точек, в которых кузнечик может оказаться, сделав 7 прыжков:
Пусть изначально кузнечик находится в точке 0.
Тогда после первого прыжка он может оказаться либо в точке 1, либо в точке -1. То есть всего 2 варианта: 1; -1.
2 прыжок: из точки 1 кузнечик может прыгнуть либо в 0, либо в 2. Из точки -1 - в точку -2 или 0. Поэтому всего 3 варианта: -2, 0, 2.
3 прыжок: из точки -2 кузнечик может попасть либо в -3, либо в -1; из точки 0 - либо в 1, либо в -1; из точки 2 - либо в 1, либо в 3. получаем 4 варианта: -3, -1, 1, 3.
4 прыжок: соответственно получаем 5 вариантов: -4, -2, 0, 2, 4.
5 прыжок: будет 6 вариантов: -5, -3, -1, 1, 3, 5.
6 прыжок: 8 вариантов: -6, -4, -5, -2, 0, 2, 4, 6.
7 прыжок: 10 вариантов: -7, -5, -3, -6, -4, -1, 1, 3, 5, 7