килограммов (так как 
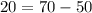). А вначале эта разница была равна 
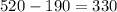килограммов.Значит, если 
часов, то разница стала равна 
. Это и будем использовать при решении задачи. a). Через 2 часа:
330 - 20 · 2 = 290 (кг)
b). Через 10 часов:
330 - 20 · 10 = 130 (кг)
c). Через 15 часов:
330 - 20 · 15 = 30 (кг)
d). Через 19 часов:
330 - 20 · 19 = - 50 (кг)
Как видим, через 19 часов муки уже будет больше на складе А.
ответ:24 руб книга а 5 руб блокнот