Пошаговое объяснение:
рассмотрим функцию
у=6х²-4х³-а
кривая бесконечно растет при х << 0 и бесконечно убывает при x >> 0
указанная функция имеет 2 экстремума
найдем их и значение функции в этих точках
y`=12x-12x²=0
x₁=0;y(0)=-a
x₂=1;y(1)=2-a
очевидно что x₂ = 1 - точка максимума
x₁=0 - точка минимума
это значит что решение уравнения у=6х²-4х³-а=0 будет единственным если 0 будет меньше чем значение функции в локальном минимуме либо больше чем значение функции в локальном максимуме
т.е.
уравнение 6х²-4х³-а=0 имеет единственный корень если -а > 0 или 2-а < 0
ответ при а < 0 и при а > 2
Задача имеет два решения.
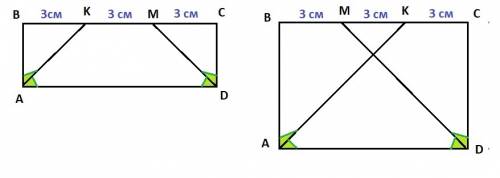
1) Прямоугольник ABCD : AK и DM - биссектрисы; BK = KM = MC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = 3 см
BC = BK + KM + MC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (3 + 9) · 2 = 24 см
P = 24 см
================================
2) Прямоугольник ABCD : AK и DM - биссектрисы; BM = MK = KC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = BM + MK = 3 + 3 = 6 см
BC = BM + MK + KC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (6 + 9) · 2 = 30 см
P = 30 см