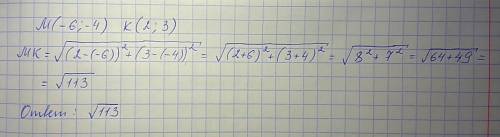
ответ: Чтобы обозначить числами точное положение точки на плоскости,
проводят две перпендикулярные координатные прямые — x и y ,
которые пересекаются в начале отсчета — точке О (смотри рисунок).
Эти прямые называют системой координат на плоскости, а точку О —
началом координат. Плоскость, на которой выбрана система координат,
называют координатной плоскостью.
Пошаговое объяснение: Пусть M — некоторая точка плоскости. Проведем через нее прямую MA ,
перпендикулярную координатной прямой X , и прямую MB ,
перпендикулярную координатной прямой Y . Так как точка A имеет
координату 4, а точка B координату 3 , то положение точки M определяется
парой чисел (4, 3) . Эту пару чисел называют координатами точки M .
Число 4 называют абсциссой точки M , а число 3 — ординатой точки M .
Координатную прямую X называют осью абсцисс,
а координатную прямую Y — осью ординат.
Точку M с абсциссой 4 и ординатой 3 обозначают так: M (4, 3) .
На первом месте пишут абсциссу точки, а на втором ее ординату.
Если переставить координаты местами, то получится другая точка
N (3, 4) , которая тоже изображена на рисунке.
Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината, и наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
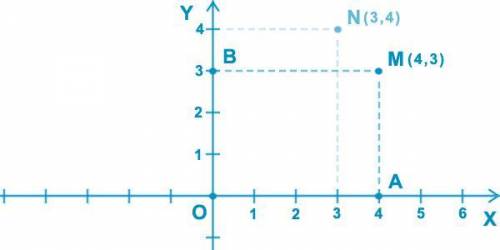
Пошаговое объяснение:
1)-14/15*25/28+(-36/37):(-6/37) =5 1/6
- 14/15 * 25/28=-(7*2)/(3*5) * (5*5)/(7*2*2)=- 5/6
-36/37 : (- 6/37)= -36/37 * (- 37/6)= 6
-5/6+ 6=5 1/6
2) в этом примере неправильно указано действие не * , а : в первом выражении
-30/31: 15/124+(-16/21)*(-7/8) = - 7 1/3
-30/31 : 15/124= -(6*5)/31: (3*5)/(31*4)=-(6*5)/31 * (31*4)/(3*5)=-8
-16/21 * (-7/8)= 2/3
-8+2/3=-7 1/3
3)26/27*(-9/65)+(-100/101):50/303 = -3 26/195
26/27 * (-9/65)=-26/195
(-100/101) : 50/303= -100/101 * 303/100=- 3
-26/195-3=-3 26/195
4)(-51/58):(-17/25)-25/27*(-81/125) = 1 259/290
(-51/58) : (-17/25)= (-17*3)/58 * (-25/17)=75/58
25/27 * (-81/125)= -3/5
75/58+3/5= 1 17/58 + 3/5=1 85/290 + 174/290=1 259/290