1. Раскроем скобки в левой части равенства:
(3x^2 + ax - b) * (x + 2) = 3x^3 + ax^2 - bx + 6x^2 + 2ax - 2b;
2. Получим равенство:
3x^3 + ax^2 + 6x^2 + 2ax - bx - 2b = 3x^3 + cx^2 + 3x - 2;
3. Сократим одинаковые члены и перенесем в левую часть все члены, содержащие множители a, b и c, а в правую - только с известными множителями:
ax^2 - cx^2 + 2ax - bx - 2b = -6x^2 + 3x - 2;
4. Т.к. равенство верно при любых x, множители в левой и правой частях перед x в одинаковой степени равны. Запишем систему равенств для a, b и c:
a - c = -6;
2a - b = 3;
2b = 2;
5. Из этих равенств получим:
b = 1;
a = (3 - 1) / 2 = 1;
c = 1 - (-6) = 7;
ответ: a = 1, b = 1, c = 7.
1) х = 16
2) х = 12
3) z = 3
4) х = 14
Пошаговое объяснение:
1) x/4 = 36/9 правую часть можно сократить
х/4 = 4 домножаем пример на знаменатель(4)
х = 16
2) 1/6 = 2/х отсюда х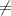
0(делить на 0 нельзя, а в примере мы делим на х), просто умножаем крестиком(1*х=2*6)
1х=12, х = 12
3) 5/z = 25/15 правую часть можно сократить z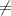0
5/z = 5/3 тут всё просто, 5делить на какое-то число = 5 делить на 3, очевидно что отсюда какое-то число(z) = 3
4) 7/4 = х/8, тут мы ничего не можем такого сделать, поэтому просто умножаем крестиком(или можно ещё домножить обе части на 8, выйдет что слева придётся умножить на два, а справа останется х, 14=х)
7*8=х*4
4х = 56
х = 14
