Пусть мальчиков, поющих в хоре было х, а девочек - у.
Из мальчиков громко пели только четверть, то есть ¼х.
Из девочек громко пели треть, то есть ⅓у.
Всего громкопоющих было 8 человек, Значит:
¼х +⅓у =8
При этом громкопоющих девочек было на две больше:
¼х+2=⅓у
Система уравнений:
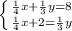
Решаем систему, подставим значение ⅓у из второго уравнения в первое:
¼х + ¼х+2 = 8
½х=8
х=16 - количество мальчиков, участвовавших в хоре.
у=3*(8-¼х)=3*(8-4)=12 - количество девочек, участвовавших в хоре.
ответ: 12 девочек и 16 мальчиков.
C(x0, 0)
(x-x0)²+(y-y0)²=R²
(-4-x0)²+(4)²=R²
(-2-x0)²+(0)²=R² ⇔ (-4-x0)²+(4)²=(-2-x0)²
16+8x0+x0²+16=4+4x0+x0²
4x0=-28 x0=-7
(-4-x0)²+(4)²=R²
(-4+7)²+16=25 ⇒R=5 (x-x0)²+(y-y0)²=R²
(x+7)²+(y)²=25