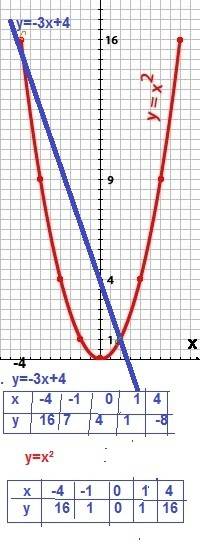
x ² =-3х+4 имеет два решения: x ₁ =1 и x ₂ =-4 .
. y=-3x+4 у=х²
х|-4|-1|0|1|4 x|-4|-1|0|1|4|
у|16|7|4|1|-8 y|16|1|0|1|16
построим графики полученных функций см приложение
Точки пересечения прямой y = -3x+4 c параболой y = x ²
имеют координаты (1; 1) и (-4; 16)
Абсциссы этих точек и являются
решением нашего уравнения
x 1 =1 , x 2 =-4 .
Проверка x ²=–3x+4 подставим наши значения вместо х
1²=-3*1+4 верно
-4²=-3*(-4)+4 верно
В решении.
Пошаговое объяснение:
Волшебная карета, которая увезла Шрека и его принцессу в свадебное путешествие, первую часть пути ехала со скоростью 22 км/ч и проехала таким образом первые 44 км пути. Затем следующие 66 км карета ехала со скоростью 44 км/ч, и наконец, последний участок протяжённостью 132 км — со скоростью 66 км/ч.
Вычислить среднюю скорость кареты на протяжении всего пути.
Формула движения: S=v*t
S - расстояние v - скорость t – время
S = 44 + 66 + 132 = 242 (км).
t= 44/22 + 66/44 + 132/66 = 2 + 1,5 + 2 = 5,5 (часа).
v = S/t
v = 242/5,5 = 44 (км/час).
y^2 должно давать такой же остаток при делении на 4, что и x^2 + 2. Но известно, что квадраты при делении на 4 дают только остатки 0 или 1, поэтому x^2 + 2 должен давать остаток 2 или 3, но тогда x^2 + 2 не может быть полным квадратом.
б) тут, например, подойдут остатки при делении на 9. Квадраты дают остатки 0 или 1 при делении на 3, тогда правая часть может давать остатки 2 + 0 = 2 или 2 + 3 = 5. Но кубы целых чисел дают остатки 0, 1 или 8 при делении на 9, так что 2 + 3y^2 не может быть точным кубом.