Сколькими различными маленький мальчик дональд может поставить в ряд четверых чёрных и 10 белых солдатиков так, чтобы чёрные солдатики не стояли рядом, если: 1) дональд различает только чёрных солдатиков (белые для него – одинаковые) 2) дональд различает только белых солдатиков (чёрные для него – одинаковые) 3) дональд различает только цвет солдатиков 4) дональд различает любых двух солдатиков.
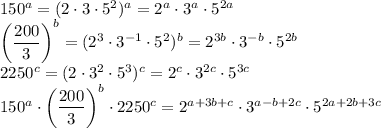
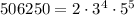 , то равенство при целых a, b, c будет в том и только в том случае, если будет выполняться система
, то равенство при целых a, b, c будет в том и только в том случае, если будет выполняться система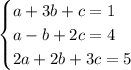
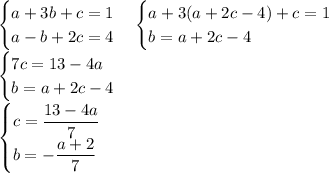
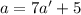 . Подставляем:
. Подставляем: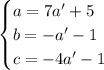
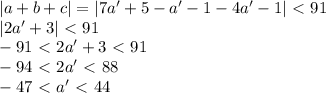
и 10 белых - Б, Б, , Б.
То что он различает только чёрных, значит что расстановка Б1 Ч1 Б2 и например Б2 Ч1 Б3 - это одно и то же.