f(x)=3cosx-4sinx+3
Выражение 3cosx-4sinx преобразуем при тождества asinx - bcosx = √(a² + b²)sin(x-arcsin(b/√(a² + b²))), где √(a² + b²) = √(4² + 3²) = √25 = 5; arcsin(b/√(a² + b²)) = arcsin(4/5). Имеем:
f(x)=3cosx-4sinx+3 = -4sinx + 3cosx +3 = 5·sin(x-arcsin(4/5)) + 3.
Значение этого выражения зависит только от первого слагаемого.
-1 ≤ sin(x-arcsin(4/5)) ≤ 1|·5; -5 ≤ 5sin(x-arcsin(4/5)) ≤ 5|+3;
-2 ≤ 5sin(x-arcsin(4/5)) + 3 ≤ 8. Т.е. -2 ≤ f(x) ≤ 8.
ответ: Е(f) = [-2; 8].
f(x)=3cosx-4sinx+3 =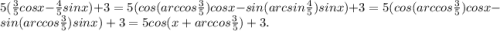 
-1 ≤ cos(x + arccos0,6) ≤ 1|·5; -5 ≤ 5cos(x + arccos0,6) ≤ 5| +3;
-2 ≤ 5cos(x + arccos0,6) + 3 ≤ 8; -2 ≤ f(x) ≤ 8.
ответ: E(f) = [-2; 8].
А:В=С
А - делимое , В - делитель , С - частное .
Частное должно увеличиться в 6 раз, то есть вместо С должно появиться 6С ⇒ если левую часть равенства увеличили в 6 раз, то чтобы выражение не изменилось, надо и правую часть равенства увеличить в 6 раз, то есть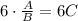 
.
Но 
.
Из равенства видно, что надо увеличить делимое А в 6 раз, а делитель В оставить без изменения, чтобы частное увеличилось в 6 раз.
Или делимое увеличить в 12 раз, а частное увеличить в 2 раза, т.к. 
, или делимое увеличить в 18 раз, а частное увеличить в 3 раза, т.к. 
, и так далее...
Но 6 можно представить и так: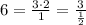 
, тогда 
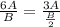. То есть делимое увеличить в 3 раза, а делитель уменьшить в 2 раза. Можно было наоборот сделать: делимое увеличить в 2 раза, а делитель уменьшить в 3 раза, так как 
.
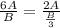x=0, x=1 есть корни
x+6=7+x нет корней
x=0 есть корень
x=1 есть корень
x=5 есть корень