Пошаговое объяснение:
В каждое из множеств D, E и F входит подмножество G, поэтому только спортом и программированием (но не математикой) увлекаются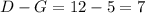 
человек, только спортом и математикой (но не программированием) увлекаются 
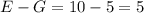человек, только программированием и математикой (но не спортом) увлекаются 
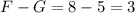человека.
Поскольку в множество A помимо учеников, увлекающихся только спортом, входят также подмножества D и E, а также их пересечение G, то количество увлекающихся только спортом можно вычислить как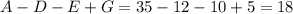 
человек. Аналогично, только программированием увлекаются 
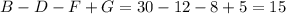человек, только математикой увлекаются 
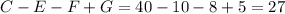человек.
Количество учеников, которые увлечены хотя бы чем-то, можно вычислить как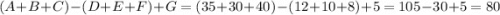 
человек, следовательно ничем не увлекаются 
человек.
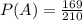
Пошаговое объяснение:
Из второго ящика наугад выбрали 1 деталь.
Переложили в 1 ящик
Вероятность, что это была стандартная деталь, составляет
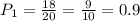
Теперь в 1 ящике 21 деталь, причем
16 - стандартных, 4 - нестандартных, и 1 с вероятностью 0.9 стандартная, а с вероятностью 0.1 нестандартная
Вероятность вытащить стандартную деталь равна вероятности вытащить из 21 деталей одну из 16 заведомо стандартных деталей
плюс вероятность вытащить положенную туда деталь умноженную на вероятность того, что она окажется стандартной
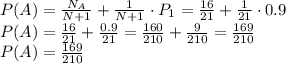
ответ: для трёх таких платьев потребуется 15 пуговиц