Надо разложить 28 кубиков в коробки по 7 кубиков в каждую.сколько потребуется коробок.

👇

Увидеть ответ

Ответ:

30kotenok04

25.07.2020

28÷7=4 (коробки)
ответ:4 коробки

4,6(82 оценок)

Ответ:

pep4

25.07.2020

Дано 28 кубиков
Нужно розложить в коробку по 7 кубиков , значит нужно:
28:7=4(коробки) - столько коробок потребуется.
ответ: 4 коробки

4,5(42 оценок)

Открыть все ответы

Ответ:

Манипуляция

25.07.2020

∠HPF = 11°.

Объяснение:

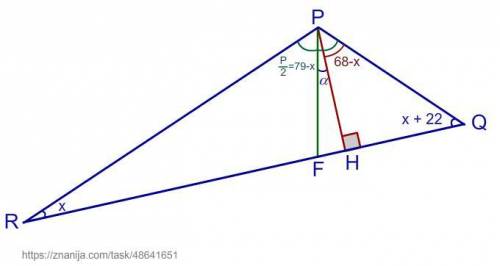
Отрезки PH и PF являются высотой и биссектрисой ΔPQR соответственно. Разность между величинами углов PQR и PRQ равна 22°. Найти угол HPF.

Дано: ΔPQR;

PH - высота;
PF - биссектриса;

∠PQR - ∠PRQ = 22°.

Найти: ∠HPF.

Решение.

1) По условию:

∠PQR - ∠PRQ = 22°.

⇒ ∠PQR = ∠PRQ + 22°.

Пусть ∠PRQ = x, тогда ∠PQR = x + 22°.

Сумма углов в треугольнике равна 180°

2) В ΔPQR

∠PRQ = x;

∠PQR = x + 22°;

∠QPR = 180° - x - (x + 22°) = 180° - x - x - 22° = 158 - 2x.

Биссектриса угла в треугольнике - это луч, с началом в вершине угла и делящий угол пополам.

3) По условию PF - биссектриса.
∠FPR = ∠QPF = ∠QPR : 2 = (158 - 2x) : 2 = 79 - x.

Высота - это перпендикуляр, проведенный из вершины треугольника на противоположную сторону.

4) PH - высота по условию.

ΔQPH прямоугольный. ∠PHQ = 90°, ∠PQH = x + 22°,

⇒ ∠QPH = 90° - (x + 22°) = 90° - x - 22° = 68° - x.

5) Для удобства обозначим угол между биссектрисой и высотой α.

∠HPF = α.

∠α = ∠QPF - ∠QPH;

∠α = 79 - x - (68 - x) = 79 - x - 68 + x = 11°

∠HPF = 11°.

Угол между биссектрисой и высотой равен 11°.

4,5(56 оценок)

Ответ:

Sasha808621

25.07.2020

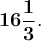
$\large \boldsymbol {} \bf 16\dfrac{1}{3} .$

Пошаговое объяснение:

Перепишем исходное выражение:

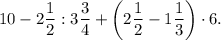$\displaystyle10-2\frac{1}{2} :3\frac{3}{4} +\bigg(2\frac{1}{2} -1\frac{1}{3}\bigg)\cdot6.$ Нужно вычислить значение выражения.

Решение: Во-первых, представим смешанные числа в виде неправильных дробей.

Правило: Результатом преобразования смешанной дроби в неправильную дробь будет дробь числитель, которой равен сумме произведения целой части на знаменатель дроби с числителем смешанной дроби, а знаменатель остается прежним.Это можно записать короче в виде формулы: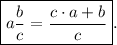 $\boxed{\displaystyle a\frac{b}{c} =\frac{c\cdot a+b}{c} } .$

В нашем случае: 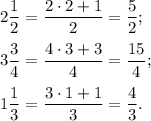$\displaystyle2\frac{1}{2} =\frac{2\cdot2+1}{2} =\frac{5}{2} ;3\frac{3}{4} =\frac{4\cdot3+3}{4} =\frac{15}{4} ;1\frac{1}{3} =\frac{3\cdot1+1}{3} =\frac{4}{3} .$

Выражение приняло вид: 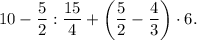$\displaystyle10-\frac{5}{2} :\frac{15}{4} +\bigg(\frac{5}{2} -\frac{4}{3} \bigg)\cdot 6.$

Первое действие - то, что в скобках.

Правило: Чтобы найти разность двух дробей с разными знаменателями, надо привести их к общему положительному знаменателю и выполнить вычитание дробей с одинаковыми знаменателями.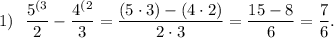

$\displaystyle1)~~\frac{5^{(3} }{2} -\frac{4^{(2} }{3} =\frac{(5\cdot3)-(4\cdot2)}{2\cdot3} =\frac{15-8}{6} =\frac{7}{6} .$

Выражение приняло вид:

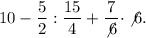$\displaystyle10-\frac{5}{2} :\frac{15}{4} +\frac{7}{\not6} \cdot\not6.$ Преобразуем.

Правило: Чтобы разделить дробь на дробь, нужно деление заменить умножением, вторую дробь "перевернуть". ⇒

$\displaystyle10-\frac{\not5}{\not2} \cdot\frac{\not4^2}{\underbrace{15}_{\not5\cdot3} } +7=10-\frac{2}{3} +7=17-\frac{2}{3} =\frac{51-2}{3} =\frac{49}{3} =\boxed{16\frac{1}{3} } .$