ответ:а)160, б)799920
Пошаговое объяснение:
Сумма цифр числа не должна делиться на 3. Цифры здесь двух типов: дающие в остатке 1 или 2. Пусть цифр первого типа k, вторых 4-k. Сумма цифр даёт тот же остаток, что и k+2(4-k)=8-k, где 0<=k<=4. Если она делится на 3, то k=2. Значит, у числа, которое делится на 3, две цифры принадлежат {1,7}, и две цифры принадлежат {2,8}.
Ясно, что имеется выбрать места для цифр первого типа (число сочетаний из 4 по 2), а когда типы заданы, двумя решить про каждую из цифр, чему она равна. Итого будет 6*2^4=96 чисел. Всего чисел из четырёх цифр имеется 4^4=256. Значит, нам подходят оставшиеся 160.
На каждом из 4 мест каждая из цифр встречается одинаковое число раз, то есть 40. Сумма в каждом разряде равна 40(1+2+7+8)=720. Умножая на 1111, имеем 799920. Это итоговая сумма.
Пошаговое объяснение:
Определяем линии.
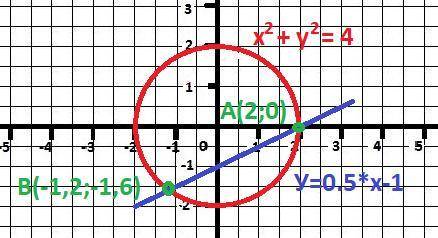
Это прямая линия и окружность радиусом R= √4 = 2
2*у = х-2 и у = 1/2*х - 1 - каноническая форму уравнения.
Рисунок к задаче в приложении.
Одна точка с явными координатами: А(2;0).
А для нахождения второй решим квадратное уравнение.
х = 2*y +2 - из уравнения прямой линии - подставим окружность.
(2*y +2)² + y² = 4
4*y² + 2*2*y*2 + 4 + y² = 4
5*y² + 8*y = 0 - квадратное уравнение - a*x² + b*x + c = 0
Вычисляем дискриминант - D.
D = b² - 4*a*c = 8² - 4*(3)*(0) = 64 - дискриминант. √D = 8.
Вычисляем корни уравнения.
у₁ = (-b+√D)/(2*a) = (-8+8)/(2*5) = 0/10 = 0 - первый корень
у₂ = (-b-√D)/(2*a) = (-8-8)/(2*5) = -16/10 = - 1,6 - второй корень
у1 = 0 и у2 = - 1,6 - координаты точек пересечения.
Вычисляем Х при У = - 1,6
х = 2*у + 2 = 2*(-1,6) + 2 = -1,2
В(-1,2;-1,6) - вторая точка пересечения - ответ.
Y= x³+2x
НАЙТИ
Уравнение касательной в точке Х0 = 1.
РЕШЕНИЕ
Уравнение касательной по формуле:
F(x) = Y'(X0)*(x - X0) + Y(X0)
Производная функции.
Y'(x) = 3x² + 2
Y'(1) = 3*1 + 2 =5
Y(1) = 1+2 = 3
Уравнение касательной
F(x) = 5*(x-1) + 3 = 5*x - 2 - ОТВЕТ
Графическое решение подтверждается рисунком в приложении.