Во времена, когда общество во главу угла ставило христианские ценности, язык канонической иконы был понятен каждому человеку, знакомому со Священным Писанием. Начиная с XVIII века в России кроме икон древнерусской и византийской школы стали появляться иконы академического письма, которые по своей сути являлись живописными картинами на библейскую тематику. Этот стиль написания пришел с Запада в послепетровский период. С тех пор многие иконы западного письма стали почитаемы в православии. Но большинство все же осталось живописью. Определим, что же такое икона и чем она отличается от картины на религиозную тему.
Площадь маленького прямоугольника внутри большого прямоугольника равна 15 м².
Пошаговое объяснение:
Надо найти площадь маленького (оранжевого) прямоугольника внутри большого.
Вспомним формулу площади прямоугольника:
Обозначим ширину искомого прямоугольника №3 - а м, высоту - b м
⇒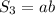
Тогда ширина прямоугольника №1 - (7-а) м,
а прямоугольника №2 - (8-а) м.
Высоты этих прямоугольников равны - b м.
А площади этих прямоугольников будут соответственно равны:
Для того, чтобы найти искомую площадь, надо найти ширину и высоту прямоугольника №3.
1. Выразим b из площади прямоугольника №1:
Подставим значение площади S₁ = 20 м² в полученное выражение:
2. Выразим b из площади прямоугольника №2:
Подставим значение площади S₂ = 25 м² в полученное выражение:
3. Приравняем выражения (1) и (2) и найдем а.
Воспользуемся основным свойством пропорции:
Произведение крайних членов равно произведению средних членов.
Раскроем скобки. Перенесем неизвестные влево, известные вправо, поменяв знак на противоположный и решим уравнение:
⇒ ширина маленького прямоугольника равна 3 м.
4. Подставим значение а=3 в (1) или (2) равенства и найдем b.
Подставим в (1):
⇒ высота маленького прямоугольника равна 5 м.
5. Теперь, зная ширину и высоту, можем найти площадь маленького прямоугольника №3:
⇒ Площадь маленького прямоугольника равна 15 м².