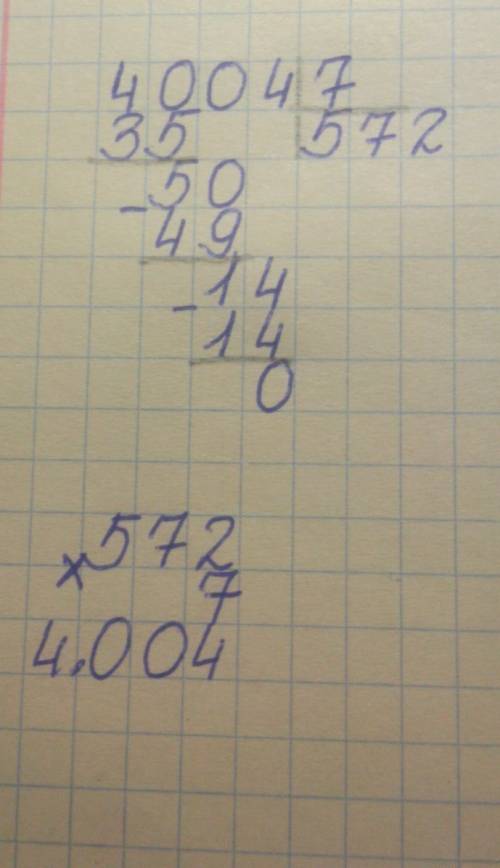
(1) (a+b)+c/(a+b)-c =7 => (a+b)+c=7*(a+b)- 7*c => 8*c = 6*(a+b) => c = (6/8)*(a+b)
(2)(a+c)+b/(a+c)-b =3,5 =>(a+c)+b=3,5*(a+c)-3,5*b => 4,5*b=2,5*(a+c) => b=(5/9)*(a+c)
Подставим в (2) выражение для с из (1), получим
(3) b=(5/9)*(a+(6/8)*(a+b)) => (9/5)*b=a+(6/8)*a+(6/8)*b => (9/5 -6/8)*b = (14/8)*a => (42/40)*b = (14/8)*a => b=(14/8 * 40/42)*a = (10/6)*a
(4) Используя (3), выразим c через а в (1)
с=(6/8)*(a+(10/6)*a) = (6/8)*a+(10/8)*a = 2*a
(5) Используя (3) и (4), имеем
(a+b+c)/(b+c-a) = (a+(10/6)*a+2*a)/((10/6)*a+2*a-a) = ((28/6)*a) / ((16/6)*a) =
= (28/6)*(6/16) = 28/16 = 7/4 = 1,75
Пошаговое объяснение:
1. 0,6(x+7)=0.5(x-3)+6.8
0.6x+7.2=0.5x-1.5+6.8
0.6x-0.5x=-4.2-1.5+6.8
0.1x=1.1
x=11
2. пусть на первой стоянке х,тогда на второй 4х После того как машины переместились,на первой стоянке стало х+35,на второй 4х-25 Составим уравнение:
4х-25=х+35
4х-х=35+25
3х=60
х=60:3
х=20 было на первой стоянке
20*4=80 было на второй.
3. Примем за х - первое число
составим и решим уравнение:
x+0,6x=48
1,6x=48
x=48:1,6
x=30 - первое число.
0,6x=0,6·30=18 - второе число.
4.
(х+2,4)/7 = (х-0,3)/3,5 по свойству пропорции
3,5 (х+2,4) = 7(х-0,3)
3,5х +8,4 =7х -2,1
3,5х -7х = -2,1 -8,4
-3,5х = - 10,5
х= -10,5 :( -3,5)
х=3
572*7=4004 (верно)