Дано: y = x⁴ - 8*x²
Исследование:
1. Область определения: D(y)= R, X∈(-∞;+∞)
2. Непрерывная. Гладкая. Вертикальных асимптот - нет
3.Поведение на бесконечности. Y(-∞)= +∞, Y(+∞)= +∞. -
4. Нули функции, пересечение с осью ОХ. Y(x)=0.
Применим метод подстановки. Z = x². z² + -8*z = 0
Нули функции: x1=-2,83, x2= x3 = 0, x4=2,83
5. Интервалы знакопостоянства.
Положительна: Y(x) ≥0 - X∈(-∞;-2.83]∪[2.83;+∞)
отрицательна: Y(x)≤0 -X∈[-2.83;2.83] .
6. Проверка на чётность. Все степени при Х: 4, 2, 0 - чётные.
Функция чётная: Y(-x) = Y(x)
7. Поиск экстремумов по первой производной.
y'(x) = 4*x³ - 16*x = 4*x*(x² - 4) = 4*x*(x-2)*(x+2) = 0
Корни производной - точки экстремумов: x₅=-2, x₆ = 0, x₇ = 2.
8. Локальные экстремумы.
Минимумы (два) при x₅ = x₇ = -2. Ymin(-2) = -16 - ответ,
Максимум (один) при х₆ = 0. Ymax(0) = 0 - ответ
Дополнительно (пригодится)
Точки перегиба в корнях второй производной.
y"(x) = 12*x² - 16 = x² - 4/3
x₈ = -√(4/3) = - 1.15, x₉ = 1.15
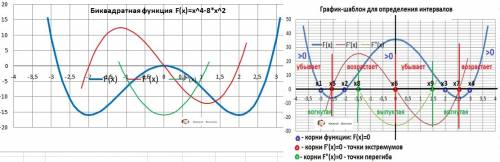
График функции и шаблон для описания - в приложении.
Пошаговое объяснение:
1) 5/9+13/27=(5*3)/(9*3)+ 13/27= 15/27+ 13/27= 28/27= 1 1/27
2) 3/8+5/24= (3*3)/(8*3) + 5/24= 9/24+ 5/24= 14/24=7/12
3 )5/12-13/72= (5*6)/(12*6) - 13/72= 30/72 - 13/72=17/72=17/72
4) 3/5-1/7= (3*7)/(5*7) - 5/(7*5)=21/35 - 5/35= 16/35
5) 5/12+1/60 = (5*5)/(12*5) +1/60= 25/60 +1/60= 26/60= 13/30
6) 9/17-19/68= (9*4)/(17*4) - 19/68= 36/68 - 19/68 =17/68 = 1/4
7) 9/10+4/15= (9*3)/(10*3) + (4*2)/(15*2)= 27/30 +8/30=35/30 = 7/6= 1 1/6
8) 4/15- 11/60= (4*4)/(15*4) - 11/60= 16/60 - 11/60 = 5/60 = 1/12
ответ:80 литров