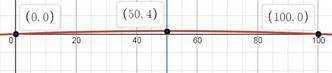
Пошаговое объяснение:
график будет такой
у = -0,0016(х-50)²+4
сместим систему координат так, чтобы центр находиля в вершине параболы (т.е. перенос по х на 50 вправо, по у на -4 (на 4 вверх))
в этой системе нарисуем "базовый" график у = -х² и увидим, что
при х = 50 у= -2500,
а нам надо 4, значит мы должны "расширить" параболу на
4/(-2500) = -0,0016 - это коэффициент а, т.е. мы уже получили часть искомого уравнения, выглядит так
у = -0,0016х²
дальше просто вернем систему координат "на родину",
т.е. на 50 влево по х и поднимем вверх на 4
и получим график
у = -0,0016(х-50)² + 4
это не хрестоматийный решения графика по точкам, классически надо брать общее уравнение у= ах² + bx + c, подставлять туда поочередно координаты трех точек и получить систему трех уравнений с тремя неизвестными а потом эту систему решать......
а строить путем смещения системы координат и быстрее и приятнее...
график полученной функции у = -0,0016(х-50)² + 4 я проверила. он удовлетворяет заданным условиям
Пошаговое объяснение:
1. Запиши в виде десятичной дроби:
11/25 = 0,44
2. Запиши обыкновенную дробь в виде десятичной:
48/1000 = 0,048
3. Преобразуй 75 мин. в часы.
Представь в виде десятичной дроби: 1,25ч
4.Запиши смешанное число в виде десятичной дроби.
19 целых 4/10 = 19,4
5. Запиши десятичную дробь в виде смешанного числа.
В результате дробь сократи: 4,25 = 4 1/4
6. Найди, какая часть фигуры не закрашена в красный цвет.
ответ: 0,7
(запиши в виде десятичной дроби).
7. Представь данную дробь 1/20 в виде десятичной дроби!
ответ:0,05
8. Запиши в виде десятичной дроби:
2 целых 1/5 = 2,2
1.4. Методические указания.
1.4.1. Определение параметров цепи
- Активное сопротивление катушки А определяем по закону Ома, согласно данных по постоянному току
- Индуктивность катушки L определяется из выражения
XL = ωL = 2π f L
где XL -индуктивное сопротивление катушки. Ом;
ω -Угловая частота; с– ;
f - частота переменного тока, Гц;
L -индуктивность (коэффициент самоиндукции), г.
В уравнении (1) два неизвестных XL можно определить из треугольника сопротивления для данной катушки, а затем определить L.
Коэффициент мощности cosφ определяется из треугольника сопротивления.
1.4.2. Параллельное соединение катушки и конденсатора.
- По закону Ома для цепи переменного тока определяются токи в ветвях с катушкой Iк и конденсатором Iс.
- Строится векторная диаграмма. Направление вектора Iк определяется углом φ согласно 1.3. Вектор тока Iк разлагается на активную Iα реактивную Ix составляющие.
- Определяются реактивный ток цепи Ix как векторная разность IL и Ic
- Сложив векторы Iq и 1k, определяем общий ток цепи I. Через масштаб находим его величину.
- Находим значение cosφ как отношение активного тока определяется полное сопротивление цепи Z.
- Определяется ток в цени Z и падения напряжения на участках UR, UL и UC.
- Вычерчиваются схема и в масштаб векторная диаграмма.
Задача 2.
В трехфазную четырехпроводную сеть включены по схеме «звезда» сопротивления: в фазу А – активное RA и индуктивное XA; в фазу В - активное RB и емкостное XB и фазу С - только активное Rс.
1.1. Ток в катушке без ферромагнитного сердечника, включенной на постоянное напряжение Un, равен Iп. Затем ее включили на переменное напряжение U частотой 50 Гц, при котором установился ток Ik..
Определить параметры катушки (R и L), коэффициент мощности cosφ и полную мощность S . Вычертить векторную диаграмму в масштабе.
1.2. Параллельно к катушке присоединили батарею конденсаторов емкостью 319мкф и включили ее на переменное напряжение частотой 50Гц. Вычертить схему. Определить ток в неразветвленной части цепи, пользуясь векторной диаграммой, коэффициент мощности cosφ и полную мощность S.
1.3. Ту же катушку и батарею конденсаторов соединили последовательно и включили на переменное напряжение, указанное выше. Определить ток в этой цепи I и вычертить схему и векторную диаграмму в масштабе.
ВариантыUn,В2,22,11,81,21,12,83,62,4Iп,А0,80,30,20,40,40,3U,ВIk,А