Задания 2,3,4 - во вложениях.
Задание 1.
а) 2,3 + х = 23 б) у - 8,9 = 1 в) 7у - 3,9 = 71,7
x = 23 - 2,3 y = 1 + 8,9 7y = 71,7 + 3,9
x = 20,7 y = 9,9 7y = 75,6
ответ: 20,7 ответ: 9,9 y = 75,6 / 7
y = 10,8
ответ: 10,8
г) х + 3х = 6 д) 12 + 8,3х + 1,5х = 95,3
4x = 6 9,8x = 95,3 - 12
x = 6 / 4 9,8x = 83,3
x = 1,5 x = 83,3 / 9,8
ответ: 1,5 x = 8,5
ответ: 8,5
Задание 5.
а) 201 - (176,4 : 16,8 + 9,68) * 2,5 = 150,55
1) 176,4 : 16,8 = 10,5
2) 10,5 + 9,68 = 20,18
3) 20,18 * 2,5 = 50,45
4) 201 - 50,45 = 150,55
ответ: 150,55
б) 0,872 * 6,3 = 5,4936
в) 0,045 * 0,1 = 0,0045
г) 7,02 : 0,065 = 108
д) 1,6 * 7,625 = 12,2
е) 30,42 : 7,8 = 3,9
ж) 0,026 : 0,01 = 2,6
Задание 6.
а) Аня купила проездной билет на месяц и сделала за месяц 41 поездку. Сколько рублей она сэкономила, если проездной билет на месяц стоит 580 рублей, а разовая поездка — 20 рублей?
Решение.
41 * 20 = 820 руб - потратила бы Аня, если каждый раз покупала билет.
820 - 580 = 240 руб - разница.
ответ: 240 руб
б) Собственная скорость теплохода 24,5 км/ч, скорость течения реки 1,3 км/ч. Сначала теплоход 0,4 ч плыл по озеру, а затем 3,5 ч по реке против течения. Какой путь теплоход за все это время?
Решение.
24,5 * 0,4 = 9,8 км - по озеру.
24,5 - 1,3 = 23,2 км/ч - скорость против течения.
23,2 * 3,5 = 81,2 км - против течения.
9,8 + 81,2 = 91 км - путь.
ответ: 91 км
в) Тетрадь стоит 14 рублей. Сколько рублей заплатит покупатель за 70 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 5% от стоимости всей покупки?
Решение.
14 * 70 = 980 руб - стоимость семидесяти тетрадей без скидки.
100% - 5% = 95% - стоимость со скидкой.
0,95 * 980 = 931 руб - стоимость семидесяти тетрадей со скидкой.
ответ: 931 руб
г) Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
Решение.
Пропорция.
800 руб - 100%
680 руб - ?%
680 * 100% : 800 = 85% - 680 руб.
100% - 85% = 15% - на это кол-во была снижена цена на футболку.
ответ: 15%
д) Цена на электрический чайник была повышена на 22% и составила 2196 рублей. Сколько рублей стоил чайник до повышения цены?
Решение.
100% - первоначальная цена.
100% + 22% = 122% - последующая цена.
Пропорция.
? руб - 100%
2196 руб - 122%
2196 * 100% : 122% = 1800 руб - первоначальная цена.
ответ: 1800 руб
е) В книге две сказки. Первая занимает в 4 раза больше страниц, чем вторая, а обе они занимают 80 страниц. Сколько страниц занимает каждая сказка?
Решение.
Пусть х страниц - занимает вторая сказка, тогда 4х страниц - занимает первая сказка. Обе они занимают 80 страниц. Составим уравнение.
4x + x = 80
5x = 80
x = 80 / 5
x = 16
16 страниц - занимает вторая сказка.
4 * 16 = 64 страницы - занимает первая сказка.
ответ: 16 страниц и 64 страницы
Задание 7.
Длина прямоугольного участка земли 125 м, а ширина 96 м. Найдите площадь поля и выразите её в арах, гектарах.
Решение.
S прямоугольного участка = a * b, где a,b - стороны прямоугольного участка.
125 * 96 = 12 000 м² - площадь прямоугольного участка.
1 ар = 100 м²
12 000 м² = 12 000 : 100 = 120 ар
1 га = 10 000 м²
12 000 м² = 12 000 : 10 000 = 1,2 га
Задание 8.
Найдите объём и площадь поверхности прямоугольного параллелепипеда, измерения которого равны 4 дм, 3 дм и 5 дм.
Решение.
V = abc, где V - объем, a,b,c - измерения.
4 * 3 * 5 = 60 дм³ - объём прямоугольного параллелепипеда.
S = 2(ab + bc + ac), где S - площадь, a,b,c - измерения.
2(4 * 3 + 3 * 5 + 4 * 5) = 2(12 + 15 + 20) = 2 * 47 = 94 дм² - площадь прямоугольного параллелепипеда.
ответ: 60 дм³ и 94 дм²
Задание 9.
Найдите среднее арифметическое чисел: 32,4; 41; 27,95; 46,9; 55,75.
Решение.

ответ: 40,8
Задание 10.
Поезд 3 ч шел со скоростью 63,2 км/ч и 4 ч со скоростью 76,5 км/ч. Найдите среднюю скорость поезда на всем пути.
Решение.
V ср = (S + S ....)/(t + t ....)
3 * 63,2 = 189,6 км сначала.
4 * 76,5 = 306 км потом.
(189,6 + 306) / (3 + 4) = 495,6 / 7 = 70,8 км/ч - средняя скорость.
ответ: 70,8 км/ч
Задание 11.
Сумма трех чисел 10,23, а среднее арифметическое шести других чисел 2,9. Найдите среднее арифметическое всех этих девяти чисел.
Решение.
Пусть а - cумма шести арифметических чисел, тогда

3 + 6 = 9 чисел - всего.
Найдем среднее арифметическое этих девяти чисел.
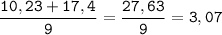
ответ: 3,07
Задание 12.
От мотка провода отрезали сначала 30 %, а затем еще 60 % остатка. После этого в мотке осталось 42 м провода. Сколько метров провода было в мотке первоначально?
Решение.
30% = 30% : 100% = 0,3
60% = 60% : 100% = 0,6
1 - 0,3 = 0,7 - остаток после первого отреза
Пусть х м - весь провод, тогда 0,3х м - отрезали сначала, потом 0,7x * 0,6 м - отрезали. И осталось 42 м провода. Составим уравнение.
x - 0,3x - 0,7x * 0,6 = 42
0,7x - 0,42x = 42
0,28x = 42
x = 42 / 0,28
x = 150
150 м - весь провод.
ответ: 150 м


еобходимое время эвакуации рассчитывается как произведение критической для человека продолжительности пожара на коэффициент безопасности. Предполагается, что каждый опасный фактор воздействует на человека независимо от других.
Критическая продолжительность пожара для людей, находящихся на этаже очага пожара, определяется из условия достижения одним из ОФП в поэтажном коридоре своего предельно допустимого значения. В качестве критерия опасности для людей, находящихся выше очага пожара, рассматривается условие достижения одним из ОФП предельно допустимого значения в лестничной клетке на уровне этажа пожара.
Значения температуры, концентраций токсичных компонентов продуктов горения и оптической плотности дыма в коридоре этажа пожара и в лестничной клетке определяются в результате решения системы уравнений теплогазообмена для помещений очага пожара, поэтажного коридора и лестничной клетки.
Уравнения движения, связывающие значения перепадов давлений на проемах с расходами через проемы, имеют вид
(13)
где G — расход через проем, кг·с -1;
m — коэффициент расхода проема ( m =0,8 для закрытых проемов и m =0,64 для открытых);
В — ширина проемов, м;
у 2, у 1 — нижняя и верхняя границы потока, м;
— плотность газов, проходящих через проем, кг·м -3,
P — средний в пределах у 2, у 1 перепад полных давлений, Па.
Нижняя и верхняя границы потока зависят от положения плоскости равных давлений
, (14)
где Р i , Р j , — статическое давление на уровне пола i -го и j -го помещений, Па;
r j r i — среднеобъемные плотности газа в j -м и i -м помещениях, кг·м -3;
g — ускорение свободного падения, м·с -2
Если плотность равных давлений располагается вне границ рассматриваемого проема ( y 0 ? h 1 или у 0 ? h 2 ), т o поток в проеме течет в одну сторону и границы потока совпадают с физическими границами проема h 1 и h 2 . Перепад давлений ( ), Па, в этом случае вычисляют по формуле
. (15)
Если плоскость равных давлений располагается в границах потока ( h 1 < y 0 < h 2 ), то в проеме текут два потока: из i -го помещения в j -е из j -г o в i -е. Нижний поток имеет границы h 1 и у 0, перепад давления для этого потока определяется по формуле
(16)
Поток в верхней части проема имеет границы y 0 и h 2 , перепад давления ( ) для него рассчитывается по формуле
(17)
Знак расхода газов (входящий в помещение расход считается положительным, выходящий — отрицательным) и значение зависят от знака перепада давлений
(18)
Уравнение баланса массы выражается зависимостью
(19)
где V j — объем помещения, м 3;
t — время, с;
Y — скорость выгорания пожарной нагрузки, кг с -1;
, — сумма расходов, входящих в помещение, кг с -1;
— сумма расходов, выходящих из помещения, кг с -1.
Уравнение энергии для коридора и лестничной клетки