Пошаговое объяснение:
ДАНО: y = (x²+4)/x
ИССЛЕДОВАНИЕ.
1. Область определения: D(y)= R\{0} , X∈(-∞;0)∪(0;+∞). Не допускаем деления на 0 в знаменателе.
2. Разрыв II-го рода при Х = 0. Вертикальных асимптота - Х = 0.
3. Наклонная асимптота: k = lim(+∞)Y(x)/x = 1
b = 0 и y(x) = x - асимптота.
4. Нули функции, пересечение с осью ОХ.
x²+4 = 0 . Нулей функции нет.
5. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(-∞;0). Положительна: Y>0 - X∈(0;+∞;)
6. Проверка на чётность.
Функция нечётная: Y(-x) = -Y(x) ,
7. Поиск экстремумов по первой производной.
y'(x) = 2 - (x²+4)/x² = (x²-4)/x² = 0.
x² - 4 = (x - 2)*(x+2) = 0
x1 = -2, x2 = 2 - точки экстремумов.
8. Локальный максимум: y(-2) = - 4, минимум: y(2) = 4.
9. Интервалы монотонности.
Возрастает - X∈(-∞;-2)∪(2;+∞). Убывает: X∈(2;0)∪(0;2).
10. Поиск перегибов по второй производной.
y"(x) = 2/x - 2*(x²-4)/x³ = 8/x³ = 0
Точки перегиба нет, кроме разрыва при Х = 0.
11. Вогнутая - "ложка"- X∈(0;+∞;), выпуклая - "горка" - X∈(-∞;0);
12. Область значений. E(y) - y∈(-∞;+∞).
13. График функции на рисунке в приложении.
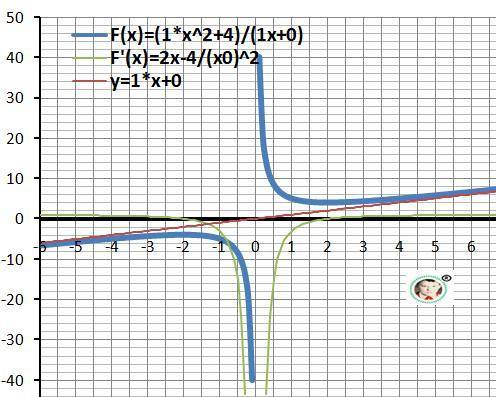
Пошаговое объяснение:
1)3*5=15 км турист за 3 часа.
2) 15/3=5 км/час (скорость пешехода).
3)
5 км/час скорость составляет 100%
х км/час составляет 1100%+100%=1200%
х=5*1200/100=60 км/час скорость поезда.
4) 60*4=240 км проехал турист на поезде.
5) 3 часа время туриста пешком составляет 100%
х час. время туриста на автобусе составляет (100+100=200% )
х=3*200/100=6часов проехал турист на автобусе.
6) скорость автобуса.
60*0,8=48 км/час.
7) Путь на автобусе.
48*6=288 км.
8) весь путь.
15+240+288=543 км.
9)
Время в пути.
3+4+6=13 часов.
10)
V=S/t=543/13= 41 10/13 ≈41 ,8 км/час. (средняя скорость туриста).