ДАНО
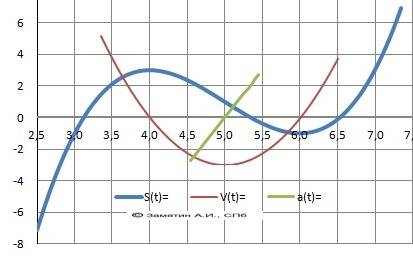
Y= x³ - 15*x² + 72*x - 109 = 0.
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
Вертикальных асимптот - нет.
2. Пересечение с осью Х. Y= 0 Корни: х₁ ≈3.12, x2 ≈ 5.35 х₃ = 6.53.
3. Пересечение с осью У. У(0) = - 109.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞.
Горизонтальной асимптоты - нет.
5. Исследование на чётность.Y(-x) ≠ - Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 3*x² - 30*х + 72 = 3*(х-4)*(х -6) = 0. .
Корни: х₁=4 , х₂ = 6.
Схема знаков производной. Функция отрицательна между корнями
_ (-∞)__(>0)__(x1=4)___(<0)___(x2=6)__(<0)_____(+∞)__
7. Локальные экстремумы.
Максимум Ymax(4)= 3, минимум – Ymin(6)= -1.
8. Интервалы монотонности.
Возрастает - Х∈(-∞;4]∪[6;+∞) , убывает = Х∈[4;6].
8. Вторая производная - Y"(x) = 6*x - 30 = 6*(x - 5)=0.
Корень производной - точка перегиба Y"(1)= 5.
9. Выпуклая “горка» Х∈(-∞;5], Вогнутая – «ложка» Х∈[5;+∞).
10. Область значений Е(у) У∈(-∞;+∞)
11. Наклонная асимптота. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(oo)Y(x)/x = ∞. Наклонной асимптоты - нет
12. График в приложении.

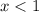
Дядя Вернон опустился на стул, дыша словно рассвирепевший носорог, его крохотные глазки, казалось, хотели пробуравить Гарри насквозь.
С самого начала летних каникул дядя Вернон обращался с ним, как с бомбой замедленного действияГарри взглянул на багровую физиономию дядюшки, побледневшее лицо тети Петуньи, которая силилась поднять с пола пыхтевшего сыночка, и тяжело вздохнул.Гарри в семье Дурслей был во всем белой вороной. Дядя Вернон — представительный мужчина с пышными, черными усами и без намека на шею. Тетя Петунья — тощая блондинка с лошадиным лицом, а розовощекий, белобрысый Дадли весьма смахивал на поросенка.
Гарри же был маленький, худенький, сквозь круглые очки на мир взирали блестящие зеленые глаза. Черные как смоль волосы вечно взъерошены, на лбу тонкий шрам, похожий на разряд молнии, — единственное свидетельство трагических событий, в результате которых одиннадцать лет назад Гарри был найден Дурслями на пороге их дома.