5/Задание № 4:
В коробке лежат шарики красного, жёлтого, зелёного, синего и белого цвета. Шариков каждого цвета разное число, не менее 1 и не более 9. Жёлтых, зелёных, синих и белых вместе - 29, а красных, жёлтых, зелёных и синих вместе - 30. Сколько красных шариков?
РЕШЕНИЕ: Так как жёлтых, зелёных, синих и белых вместе - 29, а жёлтых, зелёных, синих и красных вместе - 30, то красных шариков на 1 больше, чем белых.
Заметим, что 30 - это сумма четырех наибольших возможных значений 9+8+7+6=30. Значит, красных шариков 6, 7, 8 или 9.
Если красных шариков 9, то белых - 8, но 8 шариков уже есть - жёлтых, зелёных или синих - не может быть.
Если красных шариков 8, то белых - 7, но 7 шариков уже есть - жёлтых, зелёных или синих - не может быть.
Если красных шариков 7, то белых - 6, но 6 шариков уже есть - жёлтых, зелёных или синих - не может быть.
Если красных шариков 6, то белых – 5 – все сходится.
ОТВЕТ: 6 шариков
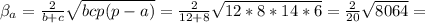 0,1*24√14 ≈ 8,979978.
0,1*24√14 ≈ 8,979978.
Всего граней кубике - 6.
Возможных вариантов бросания трех - n = 6³ = 216.
"Благоприятных вариантов набрать 5 очков - m.
Варианты:
1+1+3 - 3 варианта положения "3"
1+2 +2 - 3 варианта положения "1"
m = 6
Вероятность события по классической формуле - p = m/n = 6/216 = 1/36 ≈ 2,8% - ОТВЕТ.
2. Синий автомобиль.
Всего автомобилей - n = 20 +30 = 50.
Событие А - выбрать случайный автомобиль.
Вероятность синего - p(c) = 20/50 = 2/5 = 40% , зелёного - р(з) = 3/5 = 60% - ОТВЕТ
3. Конфета "Белочка".
Всего конфет - n = 10+5+6 = 21.
Событие А - все семь "Белочка". Вероятность такого события равна произведению каждого.
Р(А) = 10/21*9/20*8/19*7/18*6/17*5/16*4/15 = 0,48*0,45*0,42*0,39*0,35*0,31*0,27 = 0,001032 ≈ 0,1% - ОТВЕТ