Пошаговое объяснение:
1. производные
(5x³-3x⁹)' = 5*3x² -3*9x⁸ = 15x² -27x⁸
![\displaystyle (6\sqrt[3]{x} +4\sqrt{x} )' = (6x^{1/3} +4x^{1/2})'=6\frac{1}{3}x^{-2/3} +4\frac{1}{2\sqrt{x} } =\frac{2}{x^{2/3}} +\frac{2}{\sqrt{x} }](/tpl/images/1763/9786/45f1d.png)
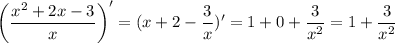
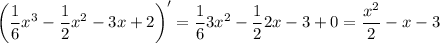
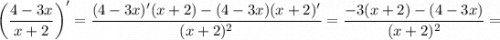

(e⁻⁵ˣ)' = -5e⁻⁵ˣ
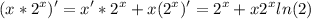
2.
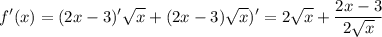
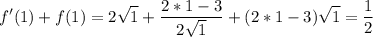
3. уравнение касательной
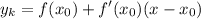
f'(x) = -2x+6
f(x₀) = f(-2) = -8
f'(x₀) = f'(-2) = 10
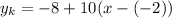
или
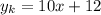
5.
для всего ниже потребуется производная
f'(x) = (x³-2x²+x+3)' = 3x² -4x +1
а) стационарные точки
3x² -4x +1 = 0 ⇒ x₁ = 1; x₂ = 1/3
б) экстремумы
f(1) = 3 - минимум
f(1/3) = 85/27 максимум
в) возрастание и убывание
по стационарным точкам получили три интервала
смотрим на каждом значение производной и определяем возрастание или убывание функции
(-∞ ;1/3) f'(0) =1 > 0 функция возрастает
(1/3; 1) f'(2/3) = -1/3 < 0 функция убывает
(1; +∞) f'(10) = 261 > 0 функция возрастает
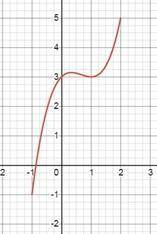
г) график прилагается (таблицу уже сами построите)
НОД (100; 300) = 100.
НОК (100, 300) = 300
Пошаговое объяснение:
НОК
Разложим на простые множители 100
100 = 2 • 2 • 5 • 5
Разложим на простые множители 300
300 = 2 • 2 • 3 • 5 • 5
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 5 , 5
Находим произведение одинаковых простых множителей и записываем ответ
НОД (100; 300) = 2 • 2 • 5 • 5 = 100
НОД
Разложим на простые множители 100
100 = 2 • 2 • 5 • 5
Разложим на простые множители 300
300 = 2 • 2 • 3 • 5 • 5
Выберем в разложении меньшего числа (100) множители, которые не вошли в разложение
Все множители меньшего числа входят в состав большего
Добавим эти множители в разложение бóльшего числа
2 , 2 , 3 , 5 , 5
Полученное произведение запишем в ответ.
НОК (100, 300) = 2 • 2 • 3 • 5 • 5 = 300
2) Только если b делится на а.
3) Это пара любых простых чисел, например 11 и 7.