При проверке учебников относительная частота качественных учебников оказалась равной 0,85. найти число бракованных книг, если всего было проверено 400 учебников.
Пусть Таня съела t конфет, Маша m конфет, а Катя k конфет. Тогда получим систему уравнений: t+m=11 m+k=15 t+k=14
Из первого уравнения t=11-m. Из второго уравнения k=15-m. Подставим эти выражения в третье уравнение: 11-m+(15-m)=14 26-2m=14 26-14=2m 2m=12 m=6 (конфет) - столько конфет съела Маша. Из первого уравнения t=11-m=11-6=5 (конфет) - столько конфет съела Таня. Из второго уравнения k=15-m=15-6=9 (конфет) - столько конфет съела Катя. Тогда общее количество съеденных конфет составит: m+t+k=6+5+9=20 (конфет).
Можно решить задачу проще: просуммируем все три уравнения системы: t+m+m+k+t+k=11+15+14 2t+2m+2k=40 2(t+m+k)=40 t+m+k=40/2=20 (конфет)
Относительная частота вычисляется по формуле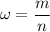
Подставим данные из условия в эту формулу.
То есть, среди 400 учебников только 340 качественных учебников, значит бракованных книг 400 - 340 = 60.
ответ: 60 книг.