1. Пусть было х трехместных и у пятиместных лодок.
x+y = 7
В трехместные лодки поместилось 3x чел, а в пятиместные 5y чел. Всего в лодках был 31 турист.
3x+5y = 31
Составим и решим систему уравнений:
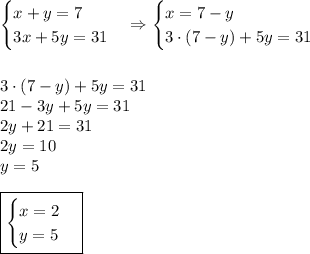 .
.
ответ: было 2 пятиместных и 5 трёхместных лодок.
2. Собственная скорость катера x км/ч, скорость течения реки y км/ч.
x+y км/ч скорость катера по течению
x-y км/ч скорость катера против течения
По течению 84 км проплыл за 3 часа:
(x+y)·3 = 84
Против течения 84 км проплыл за 3,5 часа:
(x-y)·3.5 = 84
Составим и решим систему уравнений:
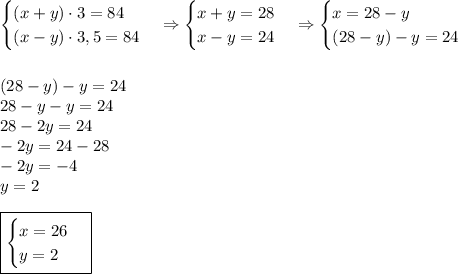
ответ: собственная скорость катера 26 км/ч, скорость течения реки 2км/ч.
1.Гоняют по кольцу. Длинна кольца 350 км. Старт и финиш в одной точке. Длинна этапа эстафеты - 75 км. Что ищем: наименьшее количество этапов. 2. А может 350 км разделится на 75 км, так что бы получилось число без остатка (что бы старт и финиш совпали) . Проверяем: 350:75=4,666... Нет не получилось. Тогда следующая точка совпадения будет - 2 круга, а это? 3. Два круга = 2 х 350км = 700 км. Может теперь разделится без остатка? Проверяем: 700:75=9,333... Нет, опять не получилось. Тогда следующая точка совпадения будет - 3 круга, а это? 4. Три круга = 3 х 350км = 1050 км. Снова ищем ровное число этапов. Проверяем: 1050:75=14. Свершилось! Ура!! ! ответ: наименьшее количество этапов 14(четырнадцать) , обоснованием ответа является решение-рассуждение.
I. Признак делимости на 10.
v Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10.
Примеры:
Числа 290, 1230, 12110 делятся на 10 без остатка.
Числа 14502, 12835, 2004 не делятся на 10 без остатка.
II. Признак делимости на 5.
v Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5. Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 5.
Примеры:
Числа 295, 12700, 12110 делятся на 5 без остатка.
Числа 14502, 12835, 2004 не делятся на 5 без остатка.
III. Признак делимости на 2.
v Если запись натурального числа оканчивается четной цифрой, то это число делится без остатка на 2. Если запись натурального числа оканчивается нечетной цифрой, то оно не делится без остатка на 2.
0, 2, 4, 6, 8 – четные цифры.
1, 3, 5, 7, 9 – нечетные цифры.
Опр. Числа, делящиеся без остатка на 2, называются четными.
Опр. Числа, которые при делении на 2 дают остаток 1, называются нечетными.
Примеры:
Числа 102, 390, 5794, 736, 508 делятся на 2 без остатка, т.е. являются четными.
Числа 2225, 1003, 449 не делятся на 2 без остатка, т.е. являются нечетными.
IV. Признак делимости на 2 и на 5.
v Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка и на 2, и на 5.
Примеры:
Числа 290, 12700 делятся и на 5, и на 2 без остатка.
Числа 14502, 12835, 2004 не делятся одновременно и на 5, и на 2 без остатка.