1) D(f)∈[-5;0)∪(0;1]
2) D(f)∈[0;2/3)
3) D(f)∈(2;3]
Пошаговое объяснение:
y=(1/2)^1/х + arcsin((x+2)/3)
Рассматриваем данную функцию по частям:
1) y=(1/2)^1/х
В степени стоит выражение 1/x и оно похоже на функцию,график которой и есть та самая гипербола!
Вспомним,что x≠0 или иначе на ноль делить нельзя! Поэтому точка 0 есть как первая критическая точка.
Поэтому обл. определения функции y=(1/2)^1/х является D(f)∈ (-∞;0)∪(0;+∞)
2) y=arcsin((x+2)/3)
В функции есть обратная тригон. функция y=arcsin (x).
Вспомним,что область определения такой функции является:
D(f)∈(-1;1)
Поэтому функция y=arcsin((x+2)/3) будет смещена,а поэтому область определения будет смещена.
Запишем такой неравенство используя область определения y=arcsin (x): D(f)∈(-1;1) :
-1≤x+2/3≤1
Решаем неравенство через систему:
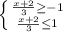
И получаем
x≤1 ; x≥-5
Тогда D(f)∈[-5;1]
В итоге построим ось x объединяя все наши расчеты:
---------*-5----------------°0------------------*1------->x
И у нас получается:
-5≤0≤1
Запишем в область определения D(f)∈[-5;0)∪(0;1]
Где * и ° - невыколотая и выколотая точка
y= e^√x * log2(2-3x)
Рассматриваем данную функцию по частям:
1)y= e^√x
В степени стоит выражение √x и оно похоже на функцию,график которой и есть та самая кривая с область определения D(f)∈[0;+∞)
Поэтому область определения y= e^√x и есть D(f)∈[0;+∞)
2)y= e^log2(2-3x)
В степени стоит выражение log2(2-3x) и найдём у этого выражения область определения так:
Логарифм-функция y=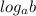 
может существовать,если b>0
Поэтому промежутот является D(f)∈(0;+∞) областью определения.
Отталкиваясь от наших выводов запишем неравенство:
2-3x>0
Решаем и получаем:
x<2/3
D(f) y= e^log2(2-3x) является промежуток : D(f)∈(-∞;2/3)
В итоге построим ось x объединяя все наши расчеты:
----------*0-------------------°2/3--------->x
Получаем,что область определения функции является промежуток :
D(f)∈[0;2/3)
Где * и ° - невыколотая и выколотая точка
3) y= arccos(x-2)-ln(x-2)
Рассматриваем данную функцию по частям:
1)y= arccos(x-2)
В функции есть обратная тригон. функция y=arccos (x).
Вспомним,что область определения такой функции является:
D(f)∈(-1;1)
Поэтому функция y=arccos(x-2) будет смещена,а поэтому область определения будет смещена.
Запишем такой неравенство используя область определения y=arcsin (x):
-1≤x-2≤1
Решаем неравенство через систему:
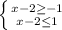
И получаем:
x≥-1 ; x≤3
Тогда D(f)∈[-1;3]
2) y=ln(x-2)
Натуральный логарифм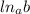 
,как и обычный логарифм имеет свойство,что b>0
Используя свойство логарифмов составим неравенство:
x-2>0
x>2
В итоге область определения этой функции:
D(f)∈(2;+∞)
Построим ось x объединяя все наши расчеты:
------------*-1--------------------°2-------------*3--------------->x
Область определения y= arccos(x-2)-ln(x-2):
D(f)∈(2;3]
Где * и ° - не выколотая и выколотая точка
Слово процент латинского происхождения и означает одну сотую часть чего-либо ( сравните цент - одна сотая доллара, центурион - начальник сотни)
1% - это одна сотая доля чего-либо.
1%=1:100=0,01
Поэтому для того, чтобы узнать содержание одного процента от целого, нужно всего лишь это целое (например, число) разделить на 100. Например,
1 процент от числа 70 это 70:100=0,7 .
1% от 700=700:100=7
или 700*0,01=7
Если процент больше одного, находят одну сотую числа и уможают на нужное количество процентов.
Пример:
3% от 300:
300:100*3=9 или 300*0,03=9
Так же находят процент от числа, выраженный не целым числом:
Число 180.
Найти 25,5% этого числа:
(180:100)*25,5= 45,9.
То есть,
чтобы найти процент от числа, нужно это число умножить на дробь, в числителе которой количество процентов, в знаменателе - 100.
Иначе:
перевести проценты в десятичную дробь (для этого следует разделить количество процентов на 100); и умножить число на эту дробь.
Так как
25,5%=0,255 ⇒
180*0,255=45,9
Целое число по проценту находят иначе.
Предположим, нужно найти число, если его 4% равны 20
Нужно найти сначала, чему равен 1%, и затем умножить содержание 1% на 100
20:4*100=500
То-есть узнать, чему равна одна сотая часть данной величины, например, числа, а затем умножить результат на 100 и получить целое, которое в 100 раз больше одной своей сотой доли.
Т.к. 4%=0,04, эта запись может выглядеть так:
20:0,04=500
Итак, чтобы найти полное число по его процентам, надо:
перевести проценты в десятичную дробь и данное число разделить на эту дробь.
m=6 количество благоприятных исходов
Вероятность равна Р=m/n=6/16=3/8=0,375