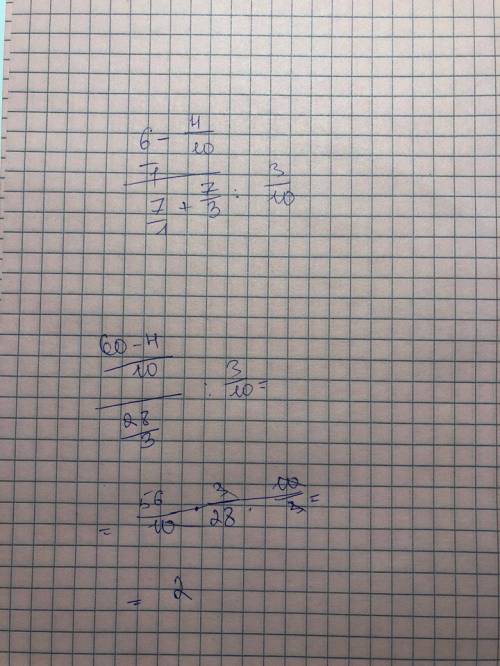
Пошаговое объяснение:
а) число всех равновозможных случаев, одно из которых обязательно произойдет при бросании монеты равно 2, так как монета имеет две стороны;
количество случаев, благоприятствующих выпадению герба равно 1, так как герб расположен только на одной стороне монеты;
вероятность выпадения герба при однократном бросании монеты равна 1/2
Для того чтобы найти какова вероятность того, чтобы хотя бы один раз выпадет герб при двух бросках монеты необходимо из 1 вычесть вероятность не выпадения герба при двух бросках монеты.
Вероятность не выпадения герба при однократном бросании монеты равна 1/2
вероятность не выпадения герба при втором броске монеты так же равна 1/2
вероятность не выпадения герба при двух бросках монеты равна
1/2 * 1/2 = 1/4
, тогда 1 − 1/4 = 3/4
вероятность того, чтобы хотя бы один раз выпадет герб при двух бросках монеты.
б)по аналогии с подпунктом а) Для того чтобы найти какова вероятность того, чтобы хотя бы один раз выпадет герб при трёх бросках монеты необходимо из 1 вычесть вероятность не выпадения герба при трёх бросках монеты.
Вероятность не выпадения герба при трёх бросках монеты равна
1/2 * 1/2 * 1/2 = 1/8
, тогда 1 − 1/8 = 7/8
вероятность того, чтобы хотя бы один раз выпадет герб при трёх бросках монеты.
а) 3/4
б) 7/8
1-значных чисел всего 3 ;
2-значных 3*3=9;
3-значных 3*3*3=27;
4-значных 81;
5-значных 243;
6- значных 729
всего чисел от 1 до 666666: 3+9+27+81+243+729=1092
7 - значных может быть 729*3=2187, следовательно число 7-значное;
Искомое число 2019-1092=927-ое семищначное число.
Рассмотрим соответствующее семизначное число троичной системы исчисления, при чем цифре 1 соответствует 0; цифре 2 - 1; цифре 6 - 2;
927/3=309; остаток 0;
309/3=103; остаток 0;
103/3=34; остаток 1;
34/3=11; остаток 1;
11/3=3; остаток 2;
3/3= 1; остаток 0;
1/3 =0; остаток 1;
Число в троичной системе, соответствующее искомому: 1021100;
С учетом соответствия:
2162211 - искомое число