Время Нурбола 15 минут = \frac{15}{60} =\frac{1}{4}6015=41 часа
Время Айдына 20 минут = \frac{20}{60} =\frac{1}{3}6020=31 часа
Пусть расстояние от дома до школы S
Тогда скорость Нурбола
v_1= S : \frac{1}{4} = 4Sv1=S:41=4S
Скорость Айдына
v_2= S : \frac{1}{3} = 3Sv2=S:31=3S
Скорость, с которой Нурбол догоняет Айдына
v = v₁ - v₂ = 4S - 3S = S
Айдын успел пройти за 3 минуты = \frac{3}{60} = \frac{1}{20}603=201 часа путь
S_2=v_2* \frac{1}{20} = \frac{3S}{20}S2=v2∗201=203S
Нурбол догонит Айдына через время
t = \frac{ S_2 }{v} = \frac{3S}{20} : S = \frac{3}{20} =\frac{9}{60}t=vS2=203S:S=203=609 часа
По условию задания составим уравнение расстояния произвольной точки М(х; у) от точки P(1; -1) в 2 раза меньшего, чем от точки М до прямой х = 4.
√((x-1)² + (y + 1)²) = |4 - x)|/2.
Модуль в правой части взят, чтобы длина не была отрицательной для точек, расположенных левее оси Оу.
Возведём обе части в квадрат.
x² - 2x + 1 + (y + 1)² = (16 - 8x + x²)/4,
4x² - 8x + 4 + 4(y + 1)² = 16 - 8x + x²,
Приведём подобные: 3x² + 4(y + 1)² = 12.
Разделим обе части на 12.
(3x²/12) + (4(y + 1)²)/12 = 1. Приведём к каноническому виду.
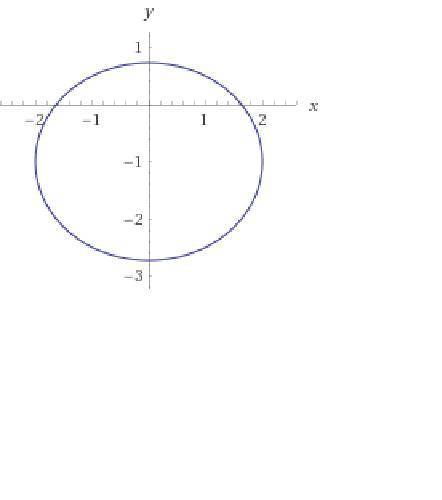
(x²/2²) + ((y + 1)²)/(√3)²) = 1.
Получено искомое уравнение. Это уравнение эллипса.
Центр её расположен в точке (0; -15).
Полуоси: действительная равна а =2, мнимая b = √3.
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
Определим параметр c: c² = a² - b² = 4 - 3 = 1 .
c = √1 = 1.
Тогда эксцентриситет будет равен: е = с/а = 1/2 .
7*3=21 прием пищи.
Завтраки: овсянка -50руб, пшенка- 30руб, манка -40руб. Того 120руб
Обеды: перловка -30руб, картошка 3кг- 40руб, курица 2.5кг- 190руб. Того 260руб.
Ужины: рис -90руб, творог -70руб, кефир 60руб, яйца- 50руб.(2ая категория). Того 270руб.
270+260+120= 650 руб.
Все это можно чередовать как угодно. Каши,крупы продаются по 500гр в среднем. Кефир 0.5л, а яиц десяток.