ответ: пуд сахара стоит 8 рублей, а фунт чая - 3 рубля.
Пусть пуд сахара стоит х, а фунт чая - y. Тогда можем составить и решить такую систему уравнений:
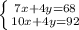
Решаем систему методом вычитания (находим x):
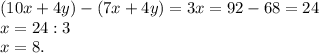
Теперь можно найти y:
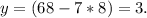
Итого: пуд сахара стоит 8 рублей, а фунт чая - 3 рубля.
Задачу можно решить и арифметически, заметив, что и там, и там по 4 фунта чаю:
1). 92 - 68 = 24 (рубля) - разница между 7 пулами и 10 пудами сахара.
2). 10 - 7 = 3 (пуда) - разница между 7 пудами и 10 пудами сахара.
3). 24 : 3 = 8 (рублей) - стоит пуд сахара.
4). (68 - 8 * 7) : 4 = 3 (рубля) - стоит фунт сахара.
Осталось подобрать S(x) таким образом, чтобы R(x) был многочленом степени не выше второй.
P(x) = ax^2 + bx + c
Q(x) = dx^2 + ex + f
Положим S(x) = gx + h, найдём g и h.
P(x) Q(x) - S(x) (x - 8)(x - 12)(x - 2017) = (ax^2 + bx + c)(dx^2 + ex + f) - (gx + h)(x - 8)(x - 12)(x - 2017)
Коэффициент при x^4:
ad - g = 0
g = ad
Коэффициент при x^3:
ae + bd - h - 8g - 12g - 2017g = 0
h = ae + bd - 2037g = ae + bd - 2037ad
g и h получились целыми числами, значит, найденный R(x) удовлетоворяет условию.