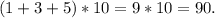
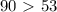, то ответ нет.
, 
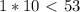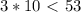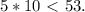
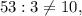
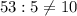и 
и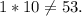 
В долине под Агармышем в 1956—1959 годах экспедиция Т. Н. Кругликовой (АН СССР) г. Москвы нашла стоянку первобытного человека, её возраст 50—70 тыс. лет. На встрече с жителями города Старый Крым, профессор М. Крамаровский сказал, что уже 14 000 лет здесь постоянно живут люди. В средние века от водосборных галерей Агармыша в долину к городу Солхат были проведены глиняные водопроводы. Таким образом Агармыш процветанию средневекового города. Часть «галерейки» (так называют местные жители старинный галерейный водопровод) функционирует до сих пор. На самом Агармыше сохранились остатки крепостной стены древнего Солхата. Именно отсюда начинал свою топографическую съёмку А. Л. Бертье-Делагард в 1925 г. для определения границ древнего города.
Вход был закрыт железобетонной плитой. Почему закрыли я не знаю.
Если будешь использовать решение, предложенное Троллем, то вот формулы:
S - площадь треугольника со сторонами a, b, с
p - его полупериметр, т.е. (a+b+c)/2
r - радиус вписанной в него окружности
sqrt(z) - функция квадратного корня из величины z
S=(r/2)*(a+b+c)
S=sqrt(p*(p-a)*(p-b)*(p-c)) //ф-ла Герона
Подставив значения, получаем:
площадь треугольника (основания пирамиды) равна 336 см, радиус вписанной окружности равен 8 см
высота пирамиды из этого тоже равна 8 см. //по т. Пифагора
x - расстояния от основания высоты пирамиды до плоскостей боковых граней равны между собой, и выражаются в данном случае так:
x = sqrt(8^2-((8*sqrt(2))/2)^2) = sqrt(32) //по т. Пифагора
x = 4*sqrt(2) - "четыре корня из двух"
Пошаговое объяснение:
