Question

Бригада рабочих устанавливает столбы освещения на шоссе. им надо установить ровно 321 столб на одной стороне шоссе. каждый следующий день им надо устанавливать по одному столбу в промежутки между уже установленными столбами. на какое наибольшее число дней бригада сможет растянуть выполнение этого ? а) 4; б) 5; в) 6; г) 7; д) 8.

Answer 1

Найдем сколько столбов установила бригада после i-ого дня.

Пусть после предыдущего (i-1) дня  стоит ровно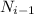 $N_{i-1}$ столбов.

Т.к. каждый следующий день столбы устанавливаются строго между уже поставленными, то в i-ый день установят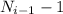 $N_{i-1} - 1$ столбов.

Тогда суммарно после i-го дня имеем:

(1) $N_i = N_{i-1} + N_{i-1} -1 = 2N_{i-1} - 1$

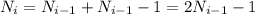
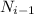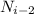Теперь, выразим  $N_{i-1}$ через  $N_{i-2}$ и подставим в выражение (1).

$N_i= 2N_{i-1} - 1 = 2(2N_{i-2}-1) - 1 = 2^2N_{i-2} - (1+2)$.

Продолжая выражать члены последовательности через предыдущие, через (i-1) шаг получим:

(2) $N_i= 2^{i-1}N_{i-(i-1)} - (1+2+...+2^{i-2})$.

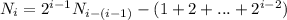В этом выражении справа видим сумму (i-1) членов геометрической прогрессии c a1=1, q=2. Ее можно также представить в виде:

$S_{i-1} = \frac{a_1 - a_1q^{i-1}}{a_1 - q} = \frac{1-2^{i-1}}{1-2} = 2^{i-1}-1$.

Подставим это в выражение (2):

(3) $N_i= 2^{i-1}N_{1} - S_{i-1} = 2^{i-1}N_{1} - 2^{i-1}+1 = 2^{i-1}(N_1-1) + 1$.

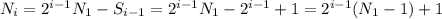Перепишем получившееся выражение в более удобном виде:

(4) $\frac{N_i-1}{N_1-1} = 2^{i-1}$.

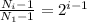Теперь мы видим, что выражение, стоящее слева знака равенства должно быть степенью 2.

По условию в конце работы: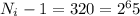 $N_i-1 = 320 = 2^6 5$

В таком случае, чтобы дробь была степенью 2, знаменатель должен быть вида:

(5)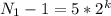 $N_1 -1 = 5* 2^k$, где k =0,1,2...

Для выполнения условия задачи, необходимо, чтобы в уравнении (4) i было максимально (чтобы работу можно было растянуть на максимальное кол-во дней). Значит нужно минимизировать знаменатель, а это значит выбрать минимальное k в выражении (5), т.е. k=0.

В таком случае: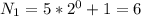 $N_1 = 5* 2^0 + 1 = 6$

Подставим это в уравнение (4):

$\frac{N_i-1}{N_1-1} = \frac{320}{5} = 64 = 2^6 = 2^{i-1}$.

Отсюда заключаем, что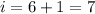 $i = 6 + 1 = 7$.

Таким образом, максимальное число дней в которые бригада сможет выполнить работу, сохраняя порядок работы, равно 7.