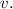Тогда скорость Феди равна 
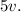Когда Федя догоняет Соню, их скорость сближения равна 
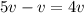(вычитаем, поскольку Соня уходит от догоняющего её Феди, тем самым, как бы мешая ему себя догонять). Когда Федя в очередной раз обгоняет Соню, его удалённость от Сони, которую он встретит в будущем, в следующем месте обгона, составляет как раз один круг. За время, пока Федя доедет до нового обгона Сони, Соня пройдет по круговой дорожке в 4 раза меньшее расстояние, поскольку её скорость в 4 раза меньше скорости сближения. Из этого и следует, что за время между двумя очередными последовательными встречами, которые разделяют участников движения расстоянием в один круг, Соня проходит только четверть круговой дорожки. Значит за 4 дополнительные встречи (после первой начальной) она и пройдёт полный круг. Т.е. всего существует 4 места, в которых малыш Федя обгоняет Соню на ходулях.
100, 110, 101 - всего 3*9 = 27 вариантов, по 3 на каждую цифру 1-9.
Если 0 нет, то первой может быть любая из двух цифр.
112, 121, 211, 122, 212, 221 - всего 6*9*8 = 432 варианта.
Вместо 1 может быть любая из цифр от 1 до 9,
вместо 2 - любая из остальных 8 цифр. Всего 8*9 = 72 варианта.
И для каждой пары цифр возможно по 6 перестановок.
Итак, всего получается 432 + 27 = 459 вариантов, но такого ответа нет.
Интересно, где я ошибся? Или ошиблись авторы задачи?